1 冒泡排序
从后往前,相邻两个比较,把小的放在前面。数次循环直到最小的已经都在前面。【冒泡把小的值逐渐的冒到最前面,一轮确定一个最小】
for(int i=0;i<arr.length;i++){
for(int j=arr.length-1;j>i;j--){
if(arr[j-1]>arr[j]){
swap(arr,j,j-1);
}
}
}
简单的改进是添加一个flag表示本次内循环中是否发生了swap,如果发生了则flag=true,而flag为false 的时候直接退出外循环,当前结果已经是最后结果。
本身有序则走一遍n就搞定,本身反序则(n-1)+(n-2)+...1=n(n-1)/2次

2 选择排序
遍历找到一个最小值,放到arr[0],再在后n-1个元素遍历,选出最小放到arr[1]...
for(int i=0;i<arr.length;i++){
for(int j=i+1;j<arr.length;j++){
if(arr[j]<arr[i]){
var t = arr[i]
arr[i]=arr[j]
arr[j]=t
}
}
}

3 插入排序
一个有序的序列,插入一个新值时,先和最后一个比较,如果大则直接放最后,如果小则和倒数第二个比,依次类推。是建立在一种原本是有序,后面插入新值的角度思考的。
var tmp, j
for (let i = 1; i < arr.length; i++) {
if (arr[i] < arr[i - 1]) {
tmp = arr[i]
for (j = i - 1; arr[j] > tmp; j--) {
arr[j + 1] = arr[j]
}
arr[j + 1] = tmp
}
}

4 希尔排序
思想为:首先将数组从中间分开,然后对应位置比较,将较小的放在前半(此时步长设为了len/2)。然后将步长缩短如变为len/4,然后还是对应位置比较,通过插入排序将越小的放在越前面。直到步长缩短为1,此时即等于插入排序。该算法通过前期跳跃性的移动节省了插入排序的交换次数,获的了比插入排序这种简单排序更好的复杂度。这个视频可以快速风趣的了解希尔排序。
var arr = [ 9, 1, 5, 8, 3, 7, 6, 4, 2]
var gap, i, j; //gap步长
var temp;
for (gap = arr.length >> 1; gap > 0; gap >>= 1){//步长一开始是数组长度/2,每次缩小一半
for (i = gap; i < arr.length; i++) {//将第一组外的数进行遍历
temp = arr[i];
//下面三行代码:每一列同一位置的元素进行比较.将较小的放在前面.插入排序,只不过步长是gap
//可以对比上面的插入排序,比较异同
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
arr[j + gap] = arr[j];
arr[j + gap] = temp;
}
}
5 堆排序
利用存储结构堆,堆是一种完全二叉树,每个节点的孩子都比自己小,这就是大顶堆,反之小顶堆。用大顶堆存储数据,然后逐个弹出根节点,就是从大到小的顺序排列。
function swap(i, j) {
var tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
function max_heapify(start, end) {
//建立父節點指標和子節點指標
var dad = start;
var son = dad * 2 + 1;
if (son >= end)//若子節點指標超過範圍直接跳出函數
return;
if (son + 1 < end && arr[son] < arr[son + 1])//先比較兩個子節點大小,選擇最大的
son++;
if (arr[dad] <= arr[son]) {//如果父節點小於子節點時,交換父子內容再繼續子節點和孫節點比較
swap(dad, son);
max_heapify(son, end);
}
}
var len = arr.length;
//初始化,i從最後一個父節點開始調整
for (var i = Math.floor(len / 2) - 1; i >= 0; i--)
max_heapify(i, len);
//先將第一個元素和已排好元素前一位做交換,再從新調整,直到排序完畢
for (var i = len - 1; i > 0; i--) {
swap(0, i);
max_heapify(0, i);
}

归并排序
分治思想,将数组中相邻俩数组成一组,一共len/2组,每组俩数排序。然后将相邻两组合并为一组,因为组内已经排好序了,所以合并的时候有些简化的操作(从a和b组中依次拿出最小的,看谁的更小,作为新组的小值,然后次小...)
Array.prototype.merge_sort = function() {
var merge = function(left, right) {
var final = [];
while (left.length && right.length)
final.push(left[0] <= right[0] ? left.shift() : right.shift());
return final.concat(left.concat(right));//当left或right中一个长度为0的时候,直接连接起来
};
var len = this.length;
if (len < 2) return this;
var mid = len / 2;
return merge(this.slice(0, parseInt(mid)).merge_sort(), this.slice(parseInt(mid)).merge_sort());
};

快速排序
同样利用分治的思想,将第一个数取出来作为mid,然后后面的和他比较,大于他的归为一组,其他归为一组。然后第一组一定是所有元素排在第二组所有元素后面的。将第这两组进行同样的操作,一直到最后每组大小为1.
Array.prototype.quick_sort = function() {
var len = this.length;
if (len <= 1)
return this.slice(0);
var left = [];
var right = [];
var mid = [this[0]];
for (var i = 1; i < len; i++)
if (this[i] < mid[0])
left.push(this[i]);
else
right.push(this[i]);
return left.quick_sort().concat(mid.concat(right.quick_sort()));
};

复杂度问题
这里时间复杂度只讨论均值。
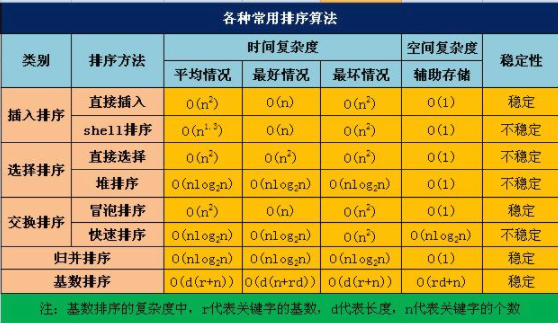
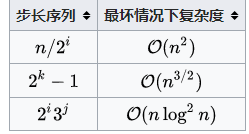
前三种为简单排序,平均时间复杂度都是O(n2)【n的平方】。shell排序在步长不同的情况下不同
堆排序时间复杂度O(nlogn),空间复杂度O(1)
归并时间复杂度O(nlogn),空间O(n)
快速时间复杂度O(nlogn),空间O(n)优化后空间复杂度更低