1 HashMap
基础知识:
- 通过数组+链表/红黑树的方式实现存储,初始容量默认是16,扩容阈值是当前容量x0.75,扩容大小是原来的两倍。
- key的hashcode对数组长度取余决定了存到哪个桶,而equals方法会在当前桶寻找key起到决定性判断作用
- 当数组大小>64且链表长度>=8的时候,会触发链表转换成红黑树
- get和put的操作复杂度都是O(1)
1.1 红黑树
红黑树是一种二叉搜索树(BST),并且是一种自平衡的BST。HashMap中树结构主要是考虑一个桶下的链表中查找元素的复杂度是O(n),而二叉搜索树可以将复杂度降低到O(logn),但是普通的二叉搜索树,会出现最差情况,退化到O(n)的情况。如下图:
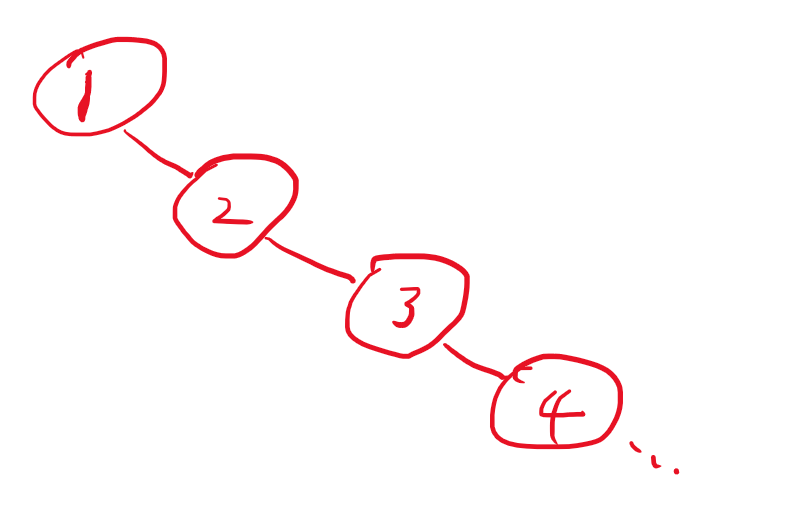
为了解决BST的失衡情况,就有了自平衡二叉树,最严格的代表就是AVL树,能保证任意节点的左子树和右子树的深度相差1以内,这样查询的复杂度就能保证最差情况也是O(logn),并且添加、删除时间复杂度都是O(logn)。然而生产环境下AVL树很少被使用,因为他的平衡条件非常严苛,这样会导致自平衡的过程会频繁触发。红黑树是对AVL树严格规则的一种弱化,红黑树的平衡规则是左右子树的深度相差2倍以内即可,弱化了平衡的标准。但是复杂度和AVL树是一致的。
1.2 为什么是2的幂次方
默认容量16,扩容是2倍,导致map一直是2的幂次方大小。这样的好处,首先我们确定index需要用key.hash对tab.size取余,如果是2的幂次方取余可以直接转为位运算(tab.size - 1) & key.hash。其次,当触发扩容的时候第i号桶的元素会分配到新的数组的第i号或者第i+oldSize号的位置里去,不会随机分配。因为code&111和code&1111其实要么相等,要么差1000也就是oldsize。
2 LinkedHashMap
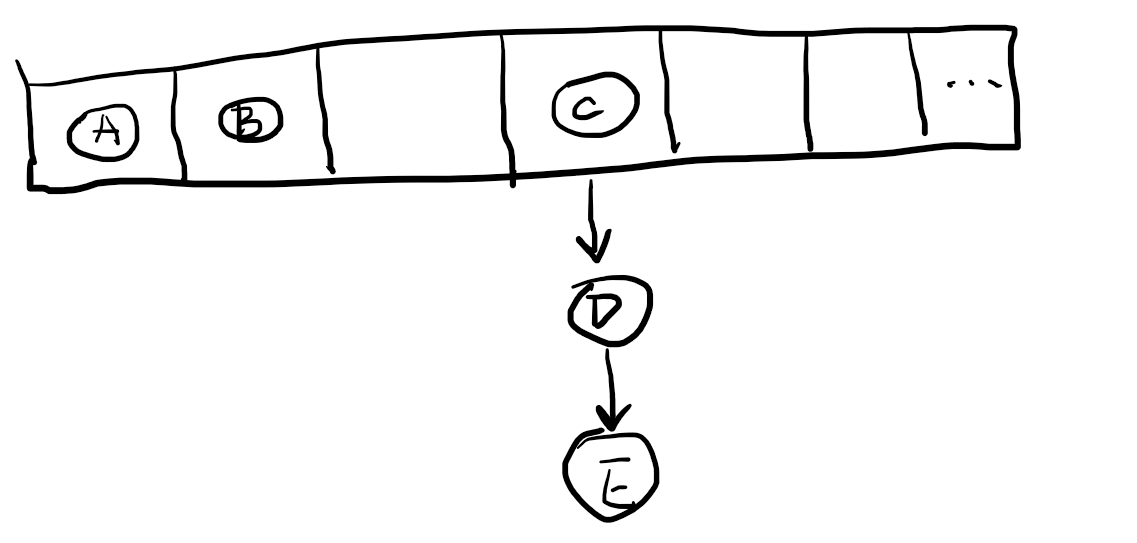
HashMap在遍历的时候会按照数组从左往右,链表从上往下依次遍历节点。而LinkedHashMap是在HashMap的基础上,对每个节点添加了一个指向下一个插入的节点的指针,形成并维护了按照插入顺序的单链表。在遍历的时候,使用该链表的iterator,遍历顺序与插入顺序一致。
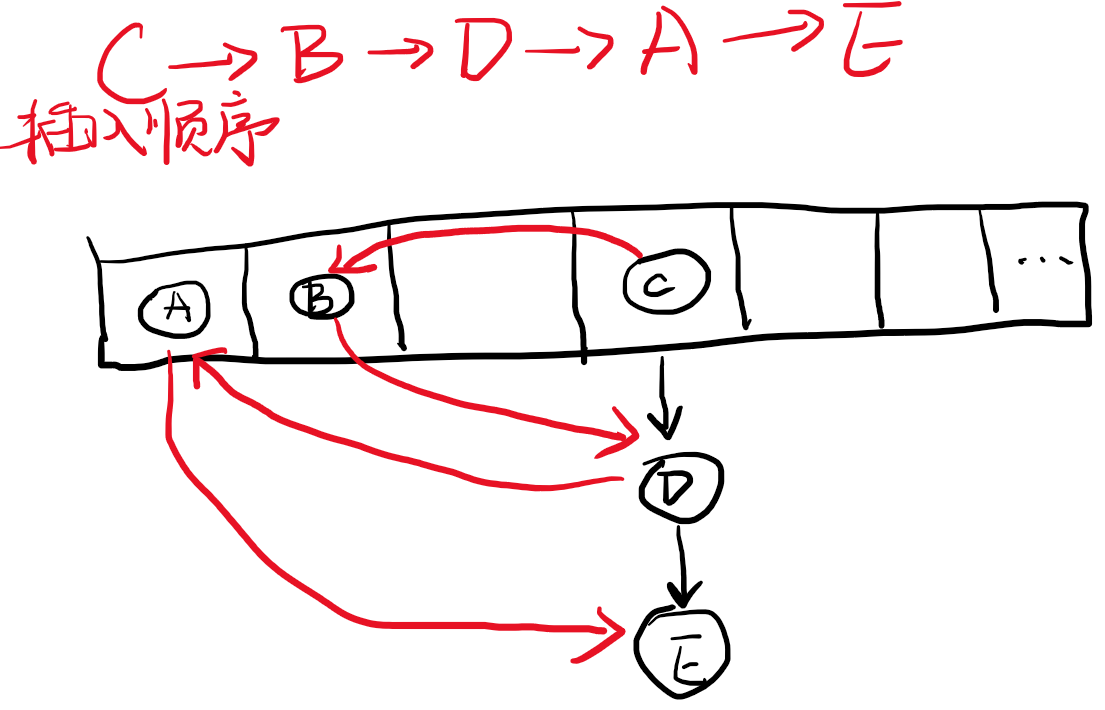
3 TreeMap
TreeMap是一颗纯红黑树,插入和查询的复杂度都成了O(logn),他主要特点是节点的有序性,会按照key的大小顺序排序。遍历的时候是按照大小顺序,从小到大迭代。
4 Hashtable
Hashtable是加锁版本的HashMap,对所有的方法添加了synchronized关键字修饰,使每一种操作都需要锁住整个数据结构,优点就是没有并发问题,缺点是锁的代价高,性能较差。
5 ConcurrentHashMap
ConcurrentHashMap是一种性能较高的并发HashMap,他的底层存储结构与HashMap一致,只不过使用了CAS和对单个桶synchronized的方法,减小了锁的范围换来了更高的性能。
有五种节点,如下。
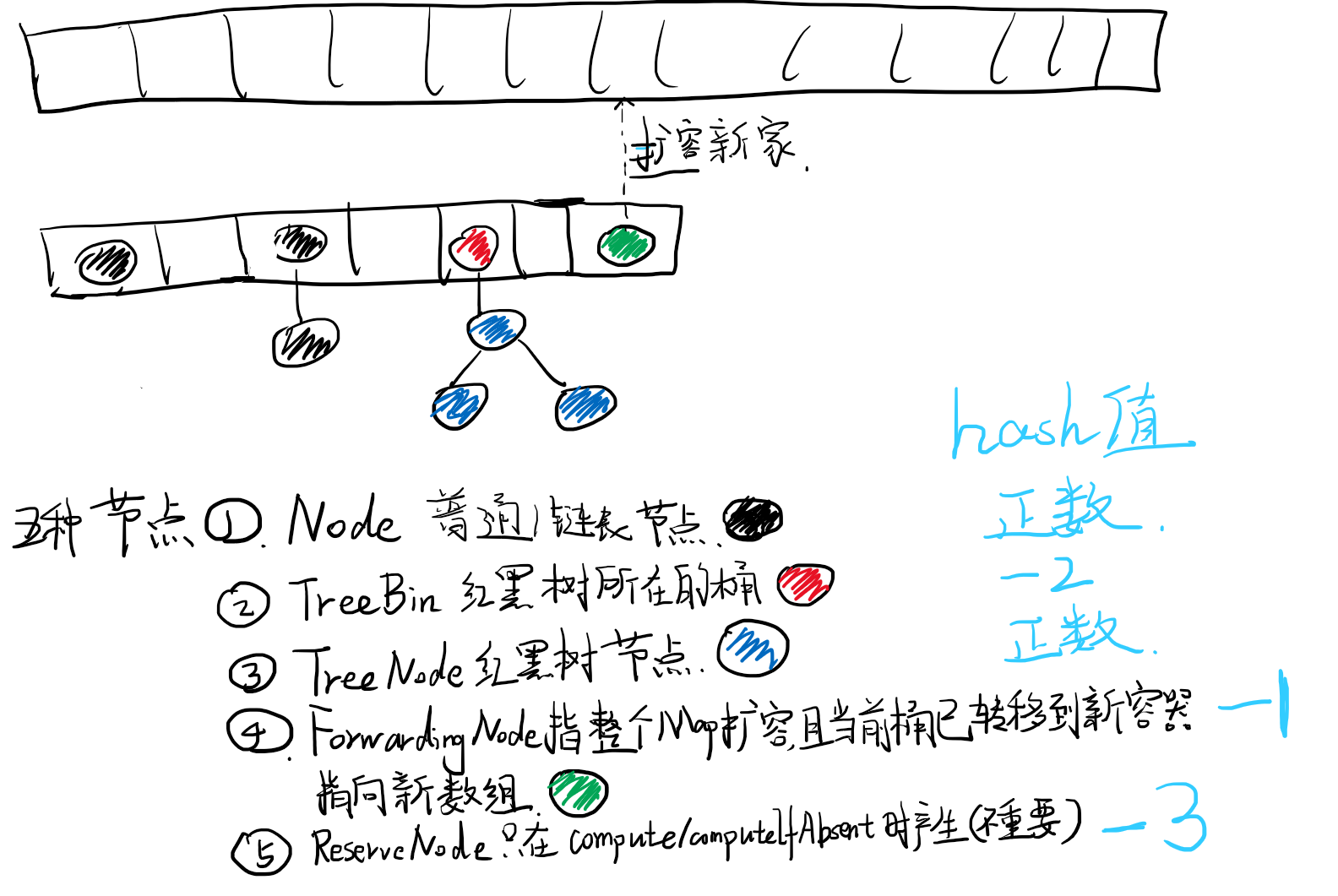
扩容的简图,如下。
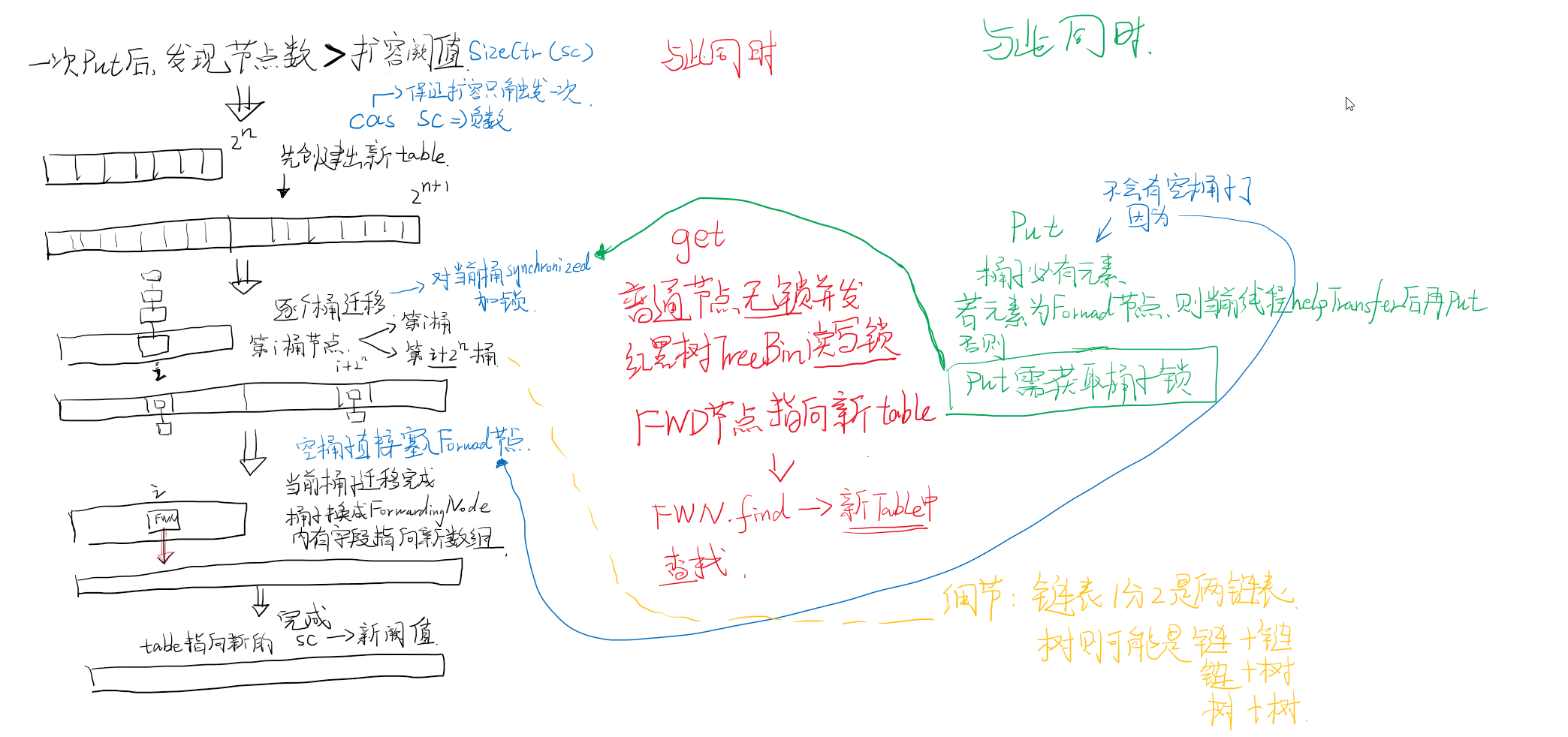
cas主要的位置
- 1 get时,当桶子里是红黑树,使用了乐观锁,防止一边Rebalance一边get
- 2 put时,当桶子是null可以直接set,用了乐观锁,防止多线程同时set当前桶子
- 3 扩容时,sizeCtl用乐观锁改为一个size相关的负数,防止多线程put同时触发了扩容。
synchronized主要的位置,都是对当前桶加锁,以下操作都是互斥的,因为他们都互相会有并发影响
- 1 put,判断当前桶子不是null,map也不在扩容时,对当前桶子加锁
- 2 transfer,扩容时,转移当前桶下的元素时,需加锁
- 3 treeifyBin,桶子从链表转成红黑树形式,需加锁
- 4 untreeifyBin,红黑树退化成链表,也需加锁
下面是代码细节,不想看可跳过。
我们简单的过一下重要方法的实现。
先来看get,get其实和HashMap的类似。对于普通的空桶或者链表,是不用加锁的,空桶返回null,链表不会有并发读写问题,因为链表都是往后追加,要么加上了要么没加上。与HashMap的不同的在于eh<0这一行,在HashMap中hash值不会小于0,而在这里是可能小于0的,小于0代表了三种节点类型。
1 正在扩容的时候,需要对每个桶的节点转移到新的数组中,如果当前桶所有节点转移完成会给桶的第一个元素塞入一个ForwardingNode节点,注意虽然叫ing其实代表自己这个桶完成了转移,其他桶还在转移进行中,其指向新的数组nextTable。他代表的是当前桶内的所有节点,已经全部安全转移到新的扩容后的数组中啦,只不过还有其他桶还在转移,所以暂时标记一下,对于这个桶的get操作,就是在nextTable中递归find操作。
2 如果桶内是树结构的话,第一个节点的hash是-2,是TreeBin类型的节点他下面挂了TreeNode才是真正的树的root节点,是持有数据的,而TreeBin的entry不持有有效数据。除了用hash=-2来作为树的判断,他主要的作用还是持有一个状态cas锁,通过其保证读写操作不会有并发的问题,因为树与list不同,树会进行restructuring自平衡调整,即当写操作触发自平衡,那么这时候的读就乱套了。因而有LOCKSTATE变量的cas操作,控制写操作需等待读操作完成之后才能触发。例如get时候的find操作就是,获取这个读写锁,之后运行root TreeNode节点的find函数。treeNode的find就和链表一样没有任何锁了。
3 ReservationNode是除了Node(普通/链表节点),ForwardingNode(扩容时会有的节点), TreeBin(树桶头元素), TreeNode(数节点)之外的一种节点,仅存在于compute/computeIfAbsent函数运行的时候,是个空节点,我们先不讨论他。
public V get(Object key) {
Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek;
// h是当前元素算出的下标
int h = spread(key.hashCode());
// e是h桶的第一个元素
if ((tab = table) != null && (n = tab.length) > 0 &&
(e = tabAt(tab, (n - 1) & h)) != null) {
// 第一个元素e.key刚好equals要找的key,那就直接返回e.val
if ((eh = e.hash) == h) {
if ((ek = e.key) == key || (ek != null && key.equals(ek)))
return e.val;
}
// eh小于0的话,有三种情况-1正在扩容,-2是tree的根节点,-3是一个受保护的节点
// 运行find方法找,对于不同节点类型的find方法是重写的
else if (eh < 0)
return (p = e.find(h, key)) != null ? p.val : null;
// 当前坑位有别人,并且hash还是正常的>0,那么就是链表一直往下找就行
while ((e = e.next) != null) {
if (e.hash == h &&
((ek = e.key) == key || (ek != null && key.equals(ek))))
return e.val;
}
}
return null;
}
上面提到了Forward也就是扩容时候的转移,而扩容发生在put的过程中,所以我们需要先了解put函数:
/** Implementation for put and putIfAbsent */
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
// 首先求出hash,算下标用
int hash = spread(key.hashCode());
int binCount = 0;
// 进入一个循环
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh; K fk; V fv;
// 数组还没初始化,就去初始化先,回来后继续循环
if (tab == null || (n = tab.length) == 0)
tab = initTable();
// 初始化了,那就用cas判断下标位置是不是null,是的话set进去,搞定
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value)))
break; // no lock when adding to empty bin
}
// MOVED是-1,也就是ForwardingNode,即所在的桶的所有节点都搬家到新tab了,
// 且有其他桶子还在搬家,那当前线程就帮其他桶子搬家,因为put得搬完了才能插入
// 所以自己闲着也是闲着,不如搭把手。
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
// onlyIfAbsent是putIfAbsent方法才是true,我们先不管这个分支
else if (onlyIfAbsent // check first node without acquiring lock
&& fh == hash
&& ((fk = f.key) == key || (fk != null && key.equals(fk)))
&& (fv = f.val) != null)
return fv;
// 如果不是正在扩容,桶首节点也有人占了,那么我们需要往后插入
// 这时候还有链表/树节点判断,各自又有不同的操作,所以直接把整个桶子锁住
else {
V oldVal = null;
synchronized (f) {
if (tabAt(tab, i) == f) {
//正常Node,就按照链表的思路找到该节点setval或者找不到就追加到最后
if (fh >= 0) {
binCount = 1;
for (Node<K,V> e = f;; ++binCount) {
K ek;
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent)
e.val = value;
break;
}
Node<K,V> pred = e;
if ((e = e.next) == null) {
pred.next = new Node<K,V>(hash, key, value);
break;
}
}
}
// 树的插入,putTreeVal中是有锁住TreeBin中的state的,因为这里的synchronized只是在put的过程中互斥,也就是对一个桶的写操作互斥
// 但是get与put不互斥,我们之前说过树的Rebalance会导致get懵逼
// 因而putTreeVal中还有一层cas锁
else if (f instanceof TreeBin) {
Node<K,V> p;
binCount = 2;
if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent)
p.val = value;
}
}
// 暂时不管这个类型的node
else if (f instanceof ReservationNode)
throw new IllegalStateException("Recursive update");
}
}
// binCount记录当前桶子节点数,主要是链表,如果链表>=8则树化
// treeifyBin中会先判断是不是tabsize>=64了,是才树化,否则就只是扩容一下
// 树化操作也会对当前桶子加synchronize锁,防止并发树化,或者并发树化+put
if (binCount != 0) {
if (binCount >= TREEIFY_THRESHOLD)//8
treeifyBin(tab, i);
if (oldVal != null)
return oldVal;
break;
}
}
}
// addCount是增加总容量的记录,该方法中还会判断是否大于sizeCtl了
// 如果大于则会触发扩容
addCount(1L, binCount);
return null;
}
扩容,读,写,删是主要的并发冲突的几个操作,get put我们上面简单介绍过了,当然还有其他的读写操作,原理类似。而扩容是非常重要的一步,我们下面着重来看下扩容的过程。首先介绍一个标志位SIZECTL这个东西看名字就知道是来控制扩容的。
- SIZECTL>0代表的是下一次扩容的阈值,上面addCount函数上说了,当大于这个值,就触发扩容
- SIZECTL
private final void addCount(long x, int check) {
......
// 当size大于sizeCtl的时候就开始扩容
while (s >= (long)(sc = sizeCtl) && (tab = table) != null &&
(n = tab.length) < MAXIMUM_CAPACITY) {
// rs一个标识,他的计算逻辑在下面
int rs = resizeStamp(n);
// sizeCtl是负数说明其他线程已经触发且正在扩容了
if (sc < 0) {
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
transferIndex <= 0)
break;
// 没啥问题的话,sc+1,当前线程也帮忙搬家
if (U.compareAndSetInt(this, SIZECTL, sc, sc + 1))
transfer(tab, nt);
}
// 正常情况下sc通过cas设置为一个n(oldsize)相关的负数,并开始扩容
else if (U.compareAndSetInt(this, SIZECTL, sc,
(rs << RESIZE_STAMP_SHIFT) + 2))
transfer(tab, null);
s = sumCount();
}
......
// n=tabsize
// Integer.numberOfLeadingZeros(n)这个int前面的0的个数,最多31个0,即1-31范围
// 然后对第15bit置1,这个的作用是上面rs << RESIZE_STAMP_SHIFT(32-16)的取值一定是负值
static final int resizeStamp(int n) {
return Integer.numberOfLeadingZeros(n) | (1 << (RESIZE_STAMP_BITS - 1));
}
transfer这个函数就非常关键了,这个代码很长,但是一定要仔细看。
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
int n = tab.length, stride;
// stride最小取16
if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE)
stride = MIN_TRANSFER_STRIDE; // subdivide range
// 这一段是new新的数组
if (nextTab == null) { // initiating
try {
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1];
nextTab = nt;
} catch (Throwable ex) { // try to cope with OOME
sizeCtl = Integer.MAX_VALUE;
return;
}
nextTable = nextTab;
transferIndex = n;
}
// 直接跳到后面实际操作的部分,下面几行不是很重要
int nextn = nextTab.length;
ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab);
boolean advance = true;
boolean finishing = false; // to ensure sweep before committing nextTab
for (int i = 0, bound = 0;;) {
Node<K,V> f; int fh;
while (advance) {
int nextIndex, nextBound;
if (--i >= bound || finishing)
advance = false;
else if ((nextIndex = transferIndex) <= 0) {
i = -1;
advance = false;
}
else if (U.compareAndSetInt
(this, TRANSFERINDEX, nextIndex,
nextBound = (nextIndex > stride ?
nextIndex - stride : 0))) {
bound = nextBound;
i = nextIndex - 1;
advance = false;
}
}
if (i < 0 || i >= n || i + n >= nextn) {
int sc;
if (finishing) {
nextTable = null;
table = nextTab;
sizeCtl = (n << 1) - (n >>> 1);
return;
}
if (U.compareAndSetInt(this, SIZECTL, sc = sizeCtl, sc - 1)) {
if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT)
return;
finishing = advance = true;
i = n; // recheck before commit
}
}
else if ((f = tabAt(tab, i)) == null)
advance = casTabAt(tab, i, null, fwd);
else if ((fh = f.hash) == MOVED)
advance = true; // already processed
else {
/*******************实际的扩容操作************************/
// 逐个桶子扩容,锁住当前桶子,使扩容的时候无法进行put和treeifyBin等操作
synchronized (f) {
if (tabAt(tab, i) == f) {
Node<K,V> ln, hn;
// fh>0正常的链表节点
if (fh >= 0) {
int runBit = fh & n;
Node<K,V> lastRun = f;
for (Node<K,V> p = f.next; p != null; p = p.next) {
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
if (runBit == 0) {
ln = lastRun;
hn = null;
}
else {
hn = lastRun;
ln = null;
}
// 当前位置的node在扩容后会放到同样的下标位置,或者i+n的位置,这样分别生成对应的两条链表
for (Node<K,V> p = f; p != lastRun; p = p.next) {
int ph = p.hash; K pk = p.key; V pv = p.val;
if ((ph & n) == 0)
ln = new Node<K,V>(ph, pk, pv, ln);
else
hn = new Node<K,V>(ph, pk, pv, hn);
}
// 将ln放到i位置,hn放到i+n位置,然后把原tab的桶子里放个forward节点,fwd指向newTab
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
// 对于树节点稍微复杂一些,对i和i+n位置存储的,可能是树,也可能需要退化成链表,其他的差不多。
else if (f instanceof TreeBin) {
TreeBin<K,V> t = (TreeBin<K,V>)f;
TreeNode<K,V> lo = null, loTail = null;
TreeNode<K,V> hi = null, hiTail = null;
int lc = 0, hc = 0;
for (Node<K,V> e = t.first; e != null; e = e.next) {
int h = e.hash;
TreeNode<K,V> p = new TreeNode<K,V>
(h, e.key, e.val, null, null);
if ((h & n) == 0) {
if ((p.prev = loTail) == null)
lo = p;
else
loTail.next = p;
loTail = p;
++lc;
}
else {
if ((p.prev = hiTail) == null)
hi = p;
else
hiTail.next = p;
hiTail = p;
++hc;
}
}
ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) :
(hc != 0) ? new TreeBin<K,V>(lo) : t;
hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) :
(lc != 0) ? new TreeBin<K,V>(hi) : t;
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
}
}
}
}
}
小结:
- put(冲突) 树化 反树化 转移是锁住当前桶子的,这些操作是互斥的。
- put(无冲突) get 是通过cas加锁或者无锁的。
- ConcurrentHashMap只是单句get/put等是线程安全的,如果有判断和操作的两步运算是不安全的
5.1 经典案例
例如简单的计数场景,没有则insert 1,有则原来基础上+1
// 常见错误用法:
// 只能保证单句函数没有并发问题的,contains这句之后,可能瞬间被其他线程remove,后面get出null
// 或者get出来的是10,但是另一个线程也执行到这一行也get了10,最后期望两个+1结果是12,但是set了11回去。
static void add(Map<String, Integer> map, String key) {
if (map.containsKey(key)) {
map.put(key, map.get(key) + 1);
} else {
map.put(key, 1);
}
}
// 正确用法,使用ConcurrentHashMap提供的有并发保障的单函数putIfAbsent来处理不包含的场景
// 然后replace这种cas配合自旋保证读取+插入的原子性
static void add(Map<String, Integer> map, String key) {
while (true) {
var oldValue = map.putIfAbsent(key, 1);
if (oldValue == null || map.replace(key, oldValue, oldValue + 1)) {
break;
}
}
}
6 scala: mutable.HashMap
scala中默认的可以修改内容的Map,他的实现按照官方的说法就是Hashtable,当然这个和java里的Hashtable类型不是一个意思,这里说的是广义上的哈希表的实现方式,也就是数组+链表的思路。如果去查看源码,https://github.com/scala/scala/blob/v2.13.10/src/library/scala/collection/mutable/HashMap.scala#L35 会发现相比java的HashMap这个要简单一些,主要是他没有红黑树,就是纯的链表,当然了本来冲突也不多的情况下,红黑树的逻辑本来也很少走到,所以这个无所谓。
另外他做了一个额外的设计,就是每个bucket下面的链表是按照原始hash值排过序的,这个有点迷,我感觉没啥用啊,插入的时候需要每个元素按照做hash的比较,不如无脑插到最后。此外get的时候因为是单链表也没法利用有序进行二分,参考L620行,是逐个遍历的,所以插入的时候会有额外的消耗,get的时候也享受不到有序的红利。
/* The HashMap class holds the following invariant:
* - For each i between 0 and table.length, the bucket at table(i) only contains keys whose hash-index is i.
* - Every bucket is sorted in ascendent hash order
* - The sum of the lengths of all buckets is equal to contentSize.
*/
7 scala immutable.HashMap
只读的HashMap在scala中使用的是Hash-Array Mapped Trie(HAMT)或者叫Hash-Array Mapped Prefix-tree(HAMP),这种数据结构主要对于只读的Map有较好的表现,对于传统的Hashtable,存在空间利用率上面的问题,例如java中HashMap底层数组最高利用率也只有75%,这也是为了保证查询复杂度,必须做出的牺牲。而对于写操作,是不改变当前对象,复制一个新对象后进行写操作。对于trie来说也可以减少复制的次数。我们先来看具体结构,最后说写时复制。
HAMT则基于Trie的思想进行构建,树的每个节点表示的是hash值的前缀,一般5个bit一组。例如对于一个key的hash值是32位的int值,那么我们把前5个bit相同的key分到一个node中,然后这个node中再去看第6-10bit相同的再分到一个node中,依次类推。例如32bit是00001 00011 00111 01111 11111 00001 11这样hash值的元素,从root节点找bitmap第1位,找到下面的node,再从这个node的bitmap中找第3位对应的node,当然中间可能就不对应一个node了,而是直接对应一个entry,只需判断key equals即可了。
如下图是一个基本的原理示意图。
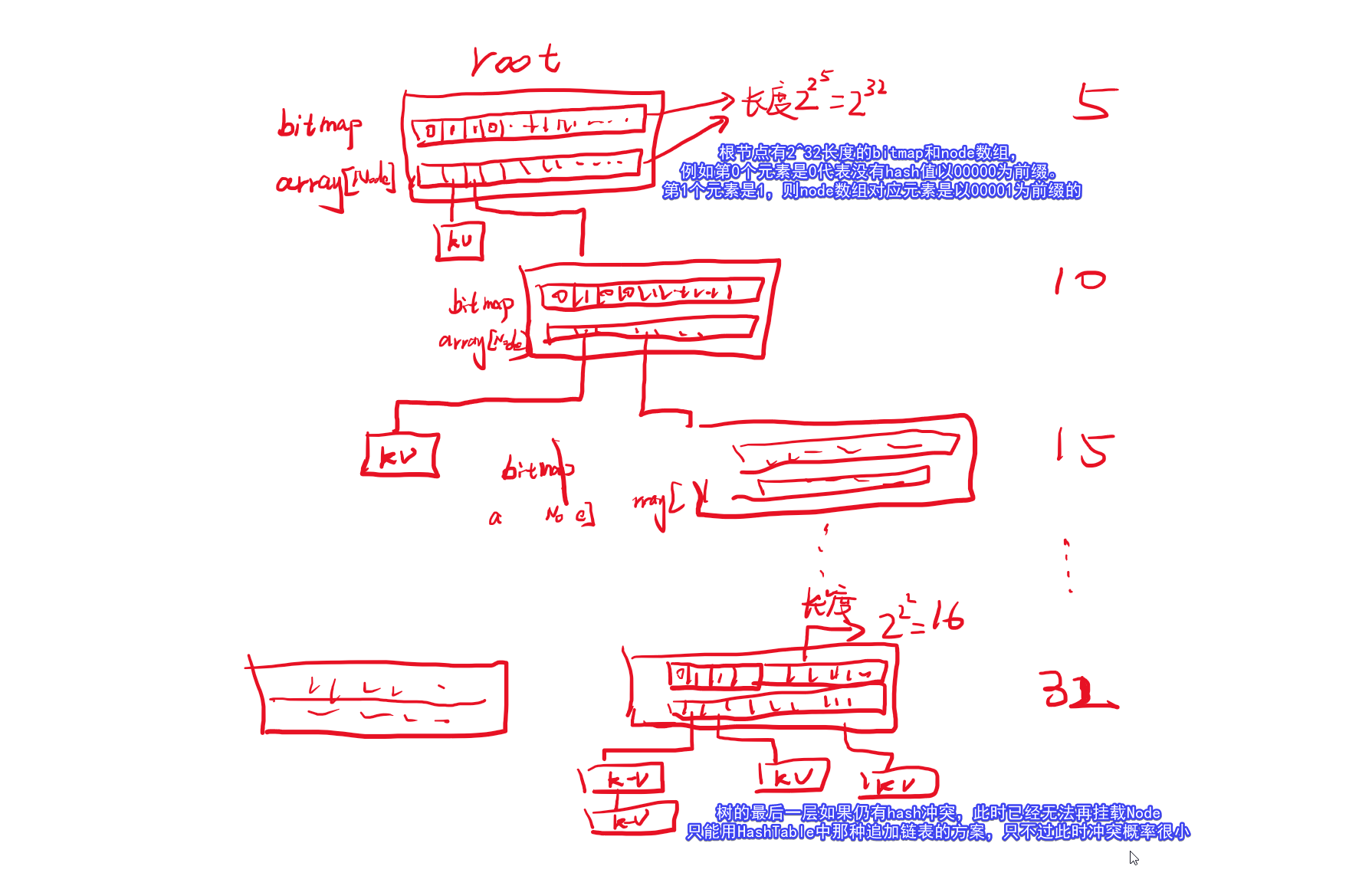
但是该图中有较大的缺陷每个Node中bitMap是2^32可以用一个4字节int就表示了,但是array的利用率可能会很低,这样申请这个大数组的利用率远低于HashTable中数组的利用率,更别提空间优化了。所以目前HAMT的常见的变种是,array的长度 = bitmap中1的个数,按顺序只把有数据的存到array中,因为bitmap可以通过位运算快速得到当前位置前面有几个1。
这样trie的空间利用率就非常高了,一个很紧凑的树状结构就出现了。但是这个树对于写操作更新array是代价很高的,有数组拷贝。所以一般用来做只读的Map,查询的时间复杂度是O(1),而空间利用更紧凑。我的评价是有点东西,但是不多。
对于Copy On Write,复制过程中Trie也有其优势。例如要insert一个hash前五bit是x的kv,而如果刚好没有已存在的元素hash前五bit是x,那么就只需要复制一份第一层的数组,后面的基本都指向原来Tree的节点。当然如果已存在元素前5位是x,那就往下直咯,其他的节点就可以保留使用其引用了。因而trie结构对于只读结构还是很有用的。在Vector结构中也能看到类似的应用。