1 解析语句
词法分析将char[]转换为了token[],接下来就是语法分析,语法分析是将token[]转换为statement[]
char[] --lex--> token[] --parse--> statement[]
语句的类型有var语句 return语句 块语句 表达式语句,暂时不考虑if/while/for等流程控制语句,其实块语句前期也用不到,也可以暂时忽略,后续再补充。(这里有人会困惑,函数声明不算是语句吗?函数声明是有返回值的表达式,返回当前函数。)先把精力聚焦于以下四种语句:
var a = <表达式>; // var语句
return <表达式>; // return语句
{ /* 其他语句 */ }// block语句
<表达式>; // expression语句
我们可以看到除了块,其他三种语句中都有一个绕不开的话题,就是表达式,表达式可以作为var语句的初始化值,也可以作为return语句的返回值,也可以作为表达式语句的表达式,语法分析最难的是表达式的解析,因为表达式可以是字面量、变量名、函数调用、还可以由操作符连接其他子表达式等等形式非常多。不过我们把表达式的解析放在第二部分,先来看如何解析上面四种语句。
这里我们借助上一节中提供的lex.mjs来开展本节的工作(当然也强烈建议先了解词法分析,再来看语法分析),定义两种主要类型Statement和AstNode,分别用来表示语句和抽象语法树节点,前者有四种语句类型也就是上面提到的var语句 return语句 块语句 表达式语句,后者AstNode我们用来表示表达式,但是暂且不需要关心如何解析表达式,只需要知道,每个表达式会被解析为一个抽象语法树节点,返回的就是root节点即可。
先声明要用到的class:
export class Statement {
constructor() {
this.endPos = -1;
}
}
export class VarStatement extends Statement {
constructor(name, value, endPos) {
super();
this.name = name; // name本身其实也是个表达式
this.value = value; // 这里的value是个表达式
this.endPos = endPos;
}
}
export class ReturnStatement extends Statement {
constructor(value, endPos) {
super();
this.value = value; // 这里的value也是表达式
this.endPos = endPos;
}
}
export class BlockStatement extends Statement {
constructor(statements, endPos) {
super();
this.statements = statements;
this.endPos = endPos;
}
}
export class ExpressionStatement extends Statement {
constructor(expression, endPos) {
super();
this.expression = expression; // 这里的expression也是表达式
this.endPos = endPos;
}
}
export class AstNode {}
export class IdentifierAstNode extends AstNode {
constructor(token) {
super();
this.token = token;
}
}
然后来写parse函数
import * as LEX from "./lex.mjs";
import {VarStatement, ReturnStatement, BlockStatement, ExpressionStatement, IdentifierAstNode, AstNode} from './parser_class_v1.mjs'
// 语法解析,把tokens转换为statements
function parse(tokens) {
var statements = [];
for (var i = 0; i < tokens.length; i++) {
var token = tokens[i];
var statement = null;
if (token.type === LEX.SEMICOLON) {
continue;
} else if (token.type === LEX.EOF || token.type === LEX.RBRACE) {
break;
} else if (token.type === LEX.VAR) {
statement = parseVarStatement(tokens, i);
} else if (token.type === LEX.RETURN) {
statement = parseReturnStatement(tokens, i);
} else if (token.type === LEX.LBRACE){
statement = parseBlockStatement(tokens, i);
} else {
statement = parseExpressionStatement(tokens, i);
}
i = statement.endPos;
statements.push(statement);
}
return statements;
}
// 从start开始转换成var语句,校验是不是var xx = xxx;格式,然后需要解析表达式parseExpression函数。
function parseVarStatement(tokens, start) {
assert(tokens[start].type === LEX.VAR, "VarStatement should start with var");
assert(tokens[start + 1].type === LEX.IDENTIFIER, "IDENTIFIER should follow var");
assert(tokens[start + 2].type === LEX.ASSIGN, "ASSIGN should follow IDENT");
var name = new IdentifierAstNode(tokens[start + 1]);
for (var i = start + 3; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var value = parseExpression(tokens, start + 3, i);
return new VarStatement(name, value, i);
}
}
}
// 与var语句类似
function parseReturnStatement(tokens, start) {
assert(tokens[start].type === LEX.RETURN, "ReturnStatement should start with return");
for (var i = start + 1; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var value = parseExpression(tokens, start + 1, i);
return new ReturnStatement(value, i);
}
}
}
// 转换为表达式语句
function parseExpressionStatement(tokens, start) {
for (var i = start; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var expression = parseExpression(tokens, start, i);
return new ExpressionStatement(expression, i);
}
}
}
// 转换为块语句
function parseBlockStatement(tokens, start) {
assert(tokens[start].type === LEX.LBRACE, "ReturnStatement should start with LBRACE");
var statements = parse(tokens.slice(start + 1));
var endPos = start + 2;
if (statements.length > 0) {
endPos = statements[statements.length - 1].endPos + 2;
}
assert(tokens[endPos].type === LEX.RBRACE, "ReturnStatement should end with RBRACE");
return new BlockStatement(statements, endPos);
}
// 这里先放置个空的逻辑,后面再补上
function parseExpression(tokens, start, end) {
return new AstNode();
}
function assert(condition, msg) {
if (!condition) {
if (msg) throw new Error(msg);
throw new Error("assert failed");
}
}
var code = `{var a = 1 + 2 * 3 / 4 - 5;}
return a;
func(a, b);
`;
var tokens = LEX.lex(code);
var statements = parse(tokens)
console.log(statements);
/* 打印:
[
BlockStatement { endPos: 14, statements: [ [VarStatement] ] },
ReturnStatement { endPos: 17, value: AstNode {} },
ExpressionStatement { endPos: 24, expression: AstNode {} }
]
*/
上面代码和测试,对应的是24.11/parser_test1.js文件的内容,但是目前有2个问题,1是转换成的对象结构,查看起来有点麻烦,我们可以给每一种Statement类型都新增toString方法;
export class Statement {
}
export class VarStatement extends Statement {
constructor(name, value) {
super();
this.name = name; // name本身其实也是个表达式
this.value = value; // 这里的value是个表达式
}
toString() {
return `var ${this.name} = ${this.value.toString()};`;
}
}
export class ReturnStatement extends Statement {
constructor(value) {
super();
this.value = value; // 这里的value也是表达式
}
toString() {
return `return ${this.value.toString()};`;
}
}
export class BlockStatement extends Statement {
constructor(statements) {
super();
this.statements = statements;
}
toString() {
return `{
${this.statements.map(it=>it.toString()).join('\n')}
}`
}
}
export class ExpressionStatement extends Statement {
constructor(expression) {
super();
this.expression = expression; // 这里的expression也是表达式
}
toString() {
return this.expression.toString() + ";";
}
}
export class AstNode {
toString() {
return `EmptyASTNode`;
}
}
export class IdentifierAstNode extends AstNode {
constructor(token) {
super();
this.token = token;
}
toString() {
return this.token.value;
}
}
2是为了记录当前解析到哪个位置了,我们在Statement类中新增一个属性endPos,这是一个解析过程中的变量,实际上不应该被语句持有,我们可以优化一下,将parseXXX语句放到parse函数中,这样下标i就是可以捕捉的变量,对i直接操作就可以了。经过优化后的代码如下,对应24.11/parser_test2.js文件的内容.
import * as LEX from "./lex.mjs";
import {VarStatement, ReturnStatement, BlockStatement, ExpressionStatement, IdentifierAstNode, AstNode} from './parser_class_v2.mjs'
function parse(tokens) {
function parseVarStatement() {
assert(tokens[i++].type === LEX.VAR, "VarStatement should start with var");
assert(tokens[i].type === LEX.IDENTIFIER, "IDENTIFIER should follow var");
var name = new IdentifierAstNode(tokens[i++]);
assert(tokens[i++].type === LEX.ASSIGN, "ASSIGN should follow IDENT");
for (var x = i; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var value = parseExpression(tokens, x, i);
return new VarStatement(name, value);
}
}
}
function parseReturnStatement() {
assert(tokens[i].type === LEX.RETURN, "ReturnStatement should start with return");
for (var x = i + 1; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var value = parseExpression(tokens, x, i);
return new ReturnStatement(value);
}
}
}
function parseExpressionStatement() {
for (var x = i; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var expression = parseExpression(tokens, x, i);
return new ExpressionStatement(expression);
}
}
}
function parseBlockStatement() {
assert(tokens[i].type === LEX.LBRACE, "ReturnStatement should start with LBRACE");
var statements = parse(tokens.slice(i + 1));
// !! 需要自己给i赋值新的结束位置,因为递归是值传递i的值
var count = 1;
for (i = i + 1; i < tokens.length; i++) {
if (tokens[i].type === LEX.LBRACE) count++;
else if (tokens[i].type === LEX.RBRACE) count--;
if (count == 0) {
break;
}
}
return new BlockStatement(statements);
}
function parseExpression(tokens, start, end) {
return new AstNode();
}
var statements = [];
for (var i = 0; i < tokens.length; i++) {
var token = tokens[i];
var statement = null;
if (token.type === LEX.SEMICOLON) {
continue;
} else if (token.type === LEX.EOF || token.type === LEX.RBRACE) {
break;
} else if (token.type === LEX.VAR) {
statement = parseVarStatement(tokens, i);
} else if (token.type === LEX.RETURN) {
statement = parseReturnStatement(tokens, i);
} else if (token.type === LEX.LBRACE){
statement = parseBlockStatement(tokens, i);
} else {
statement = parseExpressionStatement(tokens, i);
}
statements.push(statement);
}
return statements;
}
function assert(condition, msg) {
if (!condition) {
if (msg) throw new Error(msg);
throw new Error("assert failed");
}
}
var code = `{var a = 1 + 2 * 3 / 4 - 5;}
return a;
func(a, b);
`;
var tokens = LEX.lex(code);
var statements = parse(tokens);
for (var i = 0; i < statements.length; i++) {
console.log(statements[i].toString());
}
/*
打印:
{
var a = EmptyASTNode;
}
return EmptyASTNode;
EmptyASTNode;
*/
到这里我们已经把语句的解析都完成了,因为目前我们只需要考虑四种语句,接下来我们要看一下如何将上面表达式部分给解析出来,即完成parseExpression方法。
2 解析表达式
那么表达式都有哪些形式呢?
- 数字、字符串、布尔值、null、变量,这些单个值就是表达式,比如
1、"hello"、true、null、a等。 - 前缀操作符 + 另一个表达式形成新的表达式,例如
-1、!true等。 - 另一个表达式 + 后缀操作符,例如
a++、a--等。 - 二元操作符 + 左右两个表达式,例如
1 + 2、a > b、x = 1等。 - 函数调用,例如
add(a, b),注意函数的每个参数也需要是表达式。 - 括号(组group)包住子表达式,例如
(1 + 2)。 - 函数声明,在很多解释型语言中,函数声明也是表达式该表达式返回值就是函数本身,例如
var add = function(a, b) { return a + b; }。
好了,暂时想到这些,基本上涵盖了大多数表达式形式了。解析表达式的过程,就是将token[]转换为一个ast抽象语法树,例如1 + 2 * 3 / 4 - 5,最终需要解析成这样的语法树:
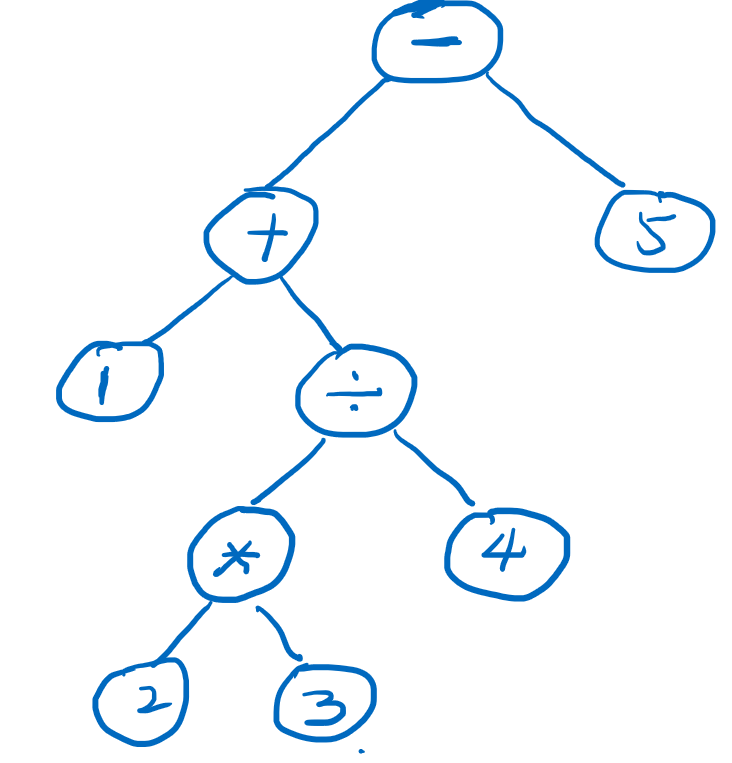
有了这样的树结构,我们才知道如何去执行这个表达式,即执行的方式和顺序,从上图中,我们就是到2 * 3先执行,然后是/4然后是1 +,最后是-5,解析表达式的两个需要考虑的重要因素是:
- 运算符的优先级,例如
*/法运算符优先级高于+-,所以要先执行乘除再执行加减。 - 运算符的结合性,例如
a + b - c,这里+和-的结合性是左结合,所以先执行a + b,然后再执行(a + b) - c,大多数都是做结合,只有赋值符号是右结合a = b = 1。
2.1 从四则运算了解中缀表达式
上述表达式的形式有点复杂,我们先来只考虑最简单的正数的四则运算的场景,思考下面的表达式,我们如何解析成上图的树状结构?有人可能想起来leetcode的算法题和逆波兰表达式了,然后就有了一些痛苦的回忆。但是我们回归零点,自己来思考。
1 + 2 * 3 / 4 - 5
2.1.1 优先级排序依次合并
从操作符的优先级去考虑,其实问题很简单,表达式只有两种token一种就是操作符,另一种是数字。我们遍历一遍节点,找到优先级最高的操作符,然后把他两边的节点挂到他的left和right上,把这个操作符标记一下已经完成了。
然后再来一次,找到剩下的操作符优先级最高的,重复上面操作,不断循环,最后数组就只剩下一个节点了,也就是我们要的树的root节点了,有点绕么?我们来看下面的操作图。
第一步,我们把token数组转成AstNode的数组,AstNode目前有数字类型和操作符类型,数字类型默认是full=true的,也就是不需要再补充额外信息啦。而操作符类型默认是full=false的,因为需要补充left和right节点,默认我们不做补充,然后我们把full的标记为绿色,not-full的标记为橘黄色。一开始数字节点都是full,操作符都是not-full,然后我们遍历AstNode[],找到优先级最高的not-full节点,这里假设*/优先级是2,+-优先级是1。会发现最高优先级的是*这个节点。
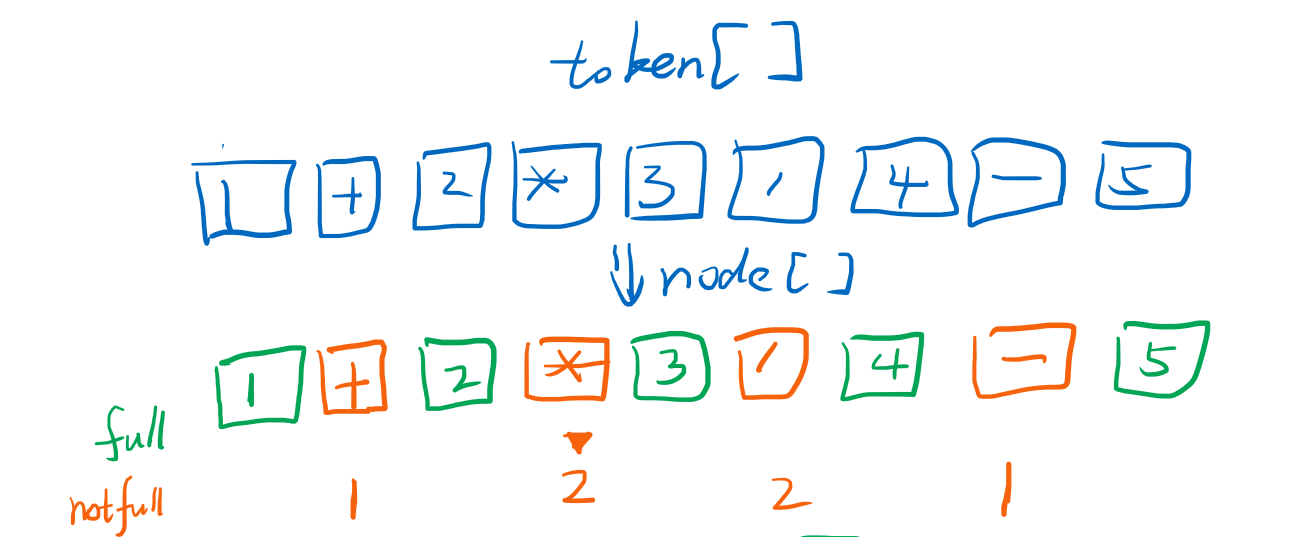
第二步,那么我们就把*节点进行填充补完,这样数组少了两个元素如下:
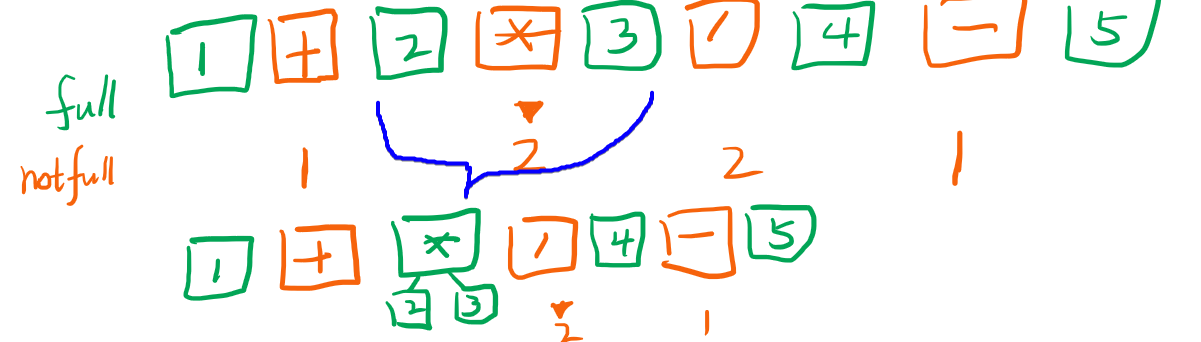
第三步,重复上面过程,发现此时最高的是/,继续合并。
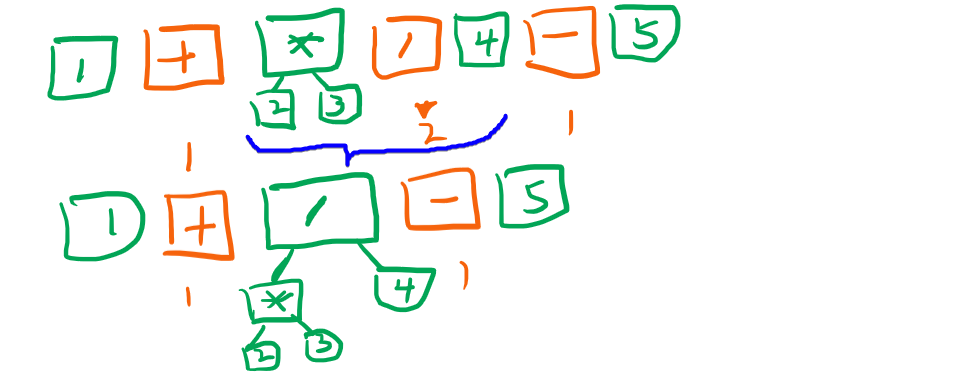
继续重复这个过程接下来就是+,然后是-,我们把这两步一起展示在途中,如下:
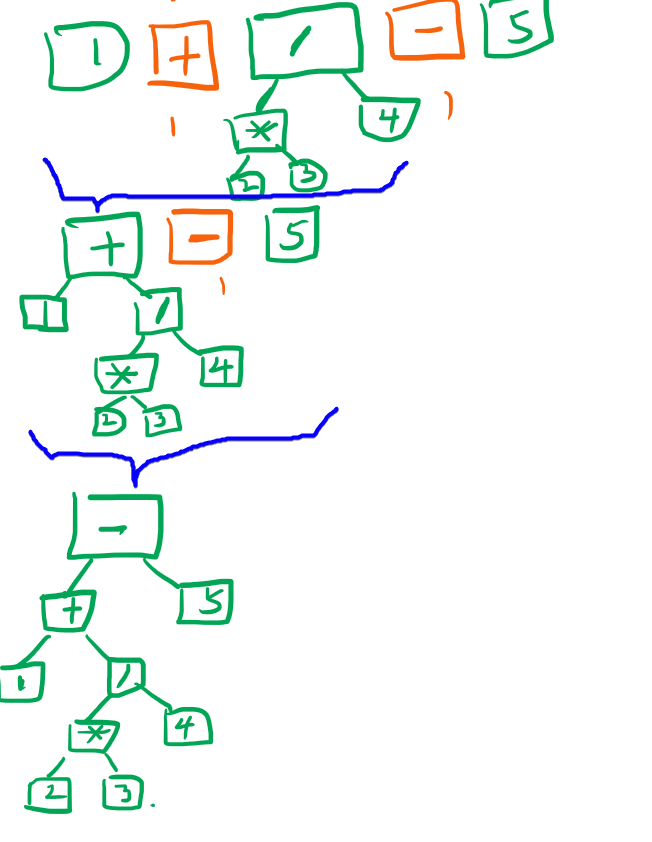
最后数组只剩下一个节点,也就是AstTree的root节点了,这是最形象,最通俗的一种解析算法,我们把代码列出:
// ....
// 这是在class_v2中补充的常量和类的定义
export const precedenceMap = {
'EOF': 0,
'+': 1,
'-': 1,
'*': 2,
'/': 2
}
export class AstNode {
constructor(full) {
if (full === undefined) this.full = false;
this.full = full;
}
toString() {
return `EmptyASTNode`;
}
}
export class IdentifierAstNode extends AstNode {
constructor(token) {
super(true);
this.token = token;
}
toString() {
return this.token.value;
}
}
export class NumberAstNode extends AstNode {
constructor(value) {
super(true);
this.value = value;
}
toString() {
return this.value;
}
}
export class InfixOperatorAstNode extends AstNode {
constructor(token) {
super(false);
this.op = token;
this.left = null;
this.right = null;
this.precedence = precedenceMap[token.value];
}
toString() {
return `(${this.left.toString()} ${this.op.value} ${this.right.toString()})`;
}
}
然后是修改parseExpression方法,创建parser_parse_exp_v1.mjs如下
import * as LEX from "./lex.mjs";
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode} from './parser_class_v2.mjs'
export function parseExpression(tokens, start, end) {
// 1 先把tokens 转成 AstNode数组
var nodes = [];
for (var i = start; i < end; i++) {
var token = tokens[i];
if (token.type === LEX.NUMBER) {
nodes.push(new NumberAstNode(token.value));
} else if (token.type === LEX.PLUS || token.type === LEX.MINUS || token.type === LEX.MULTIPLY || token.type === LEX.DIVIDE) {
var node = new InfixOperatorAstNode(token);
nodes.push(node);
} else {
throw new Error("unexpected token type: " + token.type);
}
}
// 2 数组元素不为1,则不停地遍历数组,找到最高优先级的,把两边的节点合并进来
while (nodes.length > 1) {
var maxPrecedence = -1, maxIndex = -1;
for (var i = 0; i < nodes.length; i++) {
var node = nodes[i];
if (!node.full && node.precedence > maxPrecedence) {
maxPrecedence = node.precedence;
maxIndex = i;
}
}
var maxPrecedenceNode = nodes[maxIndex];
maxPrecedenceNode.left = nodes[maxIndex - 1];
maxPrecedenceNode.right = nodes[maxIndex + 1];
maxPrecedenceNode.full = true;
// splice函数,把maxInde-1开始往后3个元素,替换为maxPrecedenceNode这一个元素
nodes.splice(maxIndex - 1, 3, maxPrecedenceNode);
}
return nodes[0];
}
我们新建一个文件24.11/parser_test3.mjs进行测试:
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode} from './parser_class_v2.mjs'
import {parseExpression} from './parser_parse_exp_v1.mjs'
// 把parseExpression方法删掉,因为从import的文件引入了,其他函数保留parser_test2.mjs
// .......
var code = `var a = 1 + 2 * 3 / 4 - 5;`;
var tokens = LEX.lex(code);
var statements = parse(tokens)
for (var i = 0; i < statements.length; i++) {
console.log(statements[i].toString());
}
/*打印
var a = ((1 + ((2 * 3) / 4)) - 5);
*/
这个方法非常的简单,对应全量代码在24.11/parser_test3.mjs。对于理解表达式解析非常有用,具有很好的教学意义,但他还是有一些问题。主要是算法的复杂度不太理想,当前的复杂度是O(n^2),还可以进行简单的优化。一种纯工程的优化方式就是,把AstNode[]数组改为双向链表,即给AstNode加两个属性prev和next。遍历token,将其append到双向链表尾部(最开始放个哨兵节点),并且如果当前节点是运算符,则塞到优先队列(堆)中,优先队列按照节点的运算优先级从高到低。这样每次从优先队列中pop取出优先级最高的节点,然后从双向链表中取出它的左右节点,放到自己的left和right属性上,然后继续从优先队列pop,重复这个过程,直到队列中没有元素。此时哨兵节点后面紧邻的一个节点就是AstTree根节点。这个优化方式非常工程化,代码也很简单,这里不展开了,感兴趣的自己简单实现下,他的复杂度是O(nlogn)。
2.1.2 Shunting Yard逆波兰
但是这个复杂度还不太够,目标是O(n),我们上面思想是从最高优先级开始合并,依次到最低优先级,所以潜在就是有排序的,排序就意味着不可能超过O(nlogn),如果要想达到O(n),那其实就是遍历一遍,而不要排序,不排序,怎么保证高优先级的先合并呢?好这里其实有一个思维定式,就是我们一直想着让最高优先级的最先合并,其实一个表达式的节点合并,并不需要最高优先级的先合并,举个例子:1 + 2 + 3 * 4,一定需要先(3*4)然后再(1+2)最后(1+2)+(3*4)吗?不,其实读取到第二个加号的时候,就可以先(1+2)了,然后读取到乘号的时候(3*4)最后(1+2)+(3*4)。其实是当我们读取到优先级小于等于前一个符号优先级的时候,就可以把前一个符号进行合并了。也就是我们不需要先找到最高优先级的,只要发现后一个符号优先级小于等于前一个,那前一个就可以进行合并操作。
上面的思路还把full这个额外字段去掉了,代码更整洁了,另外还希望把parseExpression这个函数的入参中的end给去掉,这也是一个冗余的字段,可以通过是否到了tokens结束位置,或者遇到了无法处理的token就结束表达式的识别。修改后代码如下,
import * as LEX from "./lex.mjs";
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode} from './parser_class_v2.mjs'
export function parseExpression(tokens, start) {
var nodes = [];
var opNodes = [];
for (var i = start; i < tokens.length; i++) {
var token = tokens[i];
if (token.type === LEX.NUMBER) {
nodes.push(new NumberAstNode(token.value));
} else if (token.type === LEX.PLUS || token.type === LEX.MINUS || token.type === LEX.MULTIPLY || token.type === LEX.DIVIDE) {
var node = new InfixOperatorAstNode(token);
while (opNodes.length > 0 && node.precedence <= opNodes[opNodes.length - 1].precedence) {
var opNode = opNodes.pop();
var opIndex = nodes.indexOf(opNode);
opNode.left = nodes[opIndex - 1];
opNode.right = nodes[opIndex + 1];
nodes.splice(opIndex - 1, 3, opNode);
}
nodes.push(node);
opNodes.push(node);
} else {
// 无法识别的token结束表达式识别
break;
}
}
// 遍历完之后,opNode是单调增的优先级,挨着融合即可,或者也可以整合到for循环中,用一个优先级为0的EOF哨兵节点
// 可以减少下面重复代码,但是为了更好理解,我就把这段代码摘出来放到下面了
while (opNodes.length > 0) {
var opNode = opNodes.pop();
var opIndex = nodes.indexOf(opNode);
opNode.left = nodes[opIndex - 1];
opNode.right = nodes[opIndex + 1];
nodes.splice(opIndex - 1, 3, opNode);
}
return nodes[0];
}
插一句:删除end后,其实需要对parseXXXStatement进行整改,例如当遇到var a = 1 + 1千万;这个非法语句的时候,start指向第一个1,end指向分号,需要解析的部分为1 + 1千万,然后千这里无法解析就报错了。而如果去掉end参数,会导致解析1 + 1后遇到千就返回了,并且不报错,最终的结果实际是var a = 1 + 1,为了能够处理非法语句,就需要在parseVarStatement中判断表达式解析完之后,指针是不是指向;。
这样我们只需要遍历一遍就得到结果了,不过这个代码稍微有点问题var opIndex = nodes.indexOf(opNode);这一行的复杂度是O(n)导致最终复杂度还是O(n^2),我们需要把nodes从数组改成双向链表,不过双向链表会使AstNode代码变复杂,我就不展示代码了,只需要直到改成双向链表其实复杂度就会降低到O(n)。而不展示代码的另一个原因是,还有一种更简单的写法如下,因为四则运算都是左右二元的运算符,所以上一个运算符一定位于当前nodes数组的倒数第二个位置,所以可以如下简化,此时复杂度O(n),同样把这段代码贴到parse_test3.mjs替换原来的函数,也是一样的结果。
import * as LEX from "./lex.mjs";
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode} from './parser_class_v2.mjs'
export function parseExpression(tokens, start) {
var nodes = [];
var opNodes = [];
for (var i = start; i < tokens.length; i++) {
var token = tokens[i];
if (token.type === LEX.NUMBER) {
nodes.push(new NumberAstNode(token.value));
} else if (token.type === LEX.PLUS || token.type === LEX.MINUS || token.type === LEX.MULTIPLY || token.type === LEX.DIVIDE) {
var node = new InfixOperatorAstNode(token);
while (opNodes.length > 0 && node.precedence <= opNodes[opNodes.length - 1].precedence) {
var opNode = opNodes.pop();
// opNode一定是倒数第二个元素,所以就可以简化成下面这样
opNode.right = nodes.pop();
nodes.pop();
opNode.left = nodes.pop();
nodes.push(opNode);
}
nodes.push(node);
opNodes.push(node);
} else {
break;
}
}
while (opNodes.length > 0) {
var opNode = opNodes.pop();
// opNode一定是倒数第二个元素,所以就可以简化成下面这样
opNode.right = nodes.pop();
nodes.pop();
opNode.left = nodes.pop();
nodes.push(opNode);
}
return nodes[0];
}
这其实就是逆波兰表达式的思想,当然逆波兰表达式的标准解法中,一个栈只用来存储数字,另一个只用来存储操作符,比我们上面做法要精炼,但是都是用到了一个核心思想:当新的操作符优先级小于等于栈顶操作符,则栈顶操作符可以弹出并进行合并,本质上就是单调栈的思想。
基于这种思想进行语法分析,其实又叫Shunting Yard算法,是一种最简单朴素的表达式解析的方法,他的优点就是非常简单容易理解,缺点则是:
- 1 右结合是默认不支持的,
a=b=1的场景下,上面栈的顺序,始终会在遇到第二个等号的时候,先计算a=b,需要做一些改动,即<=这里需要根据操作符进行调整是<=还是< - 2 对于复杂语法,例如函数调用,三目运算符,等,需要额外的修改才行。
- 3 对于上下文敏感的语法,基本无能为力。
2.1.3 Pratt算法
所以现代编程语言的解析器基本不适用Shunting Yard算法,而是采用了Pratt算法。我们再来聊一下Pratt的实现思想。Pratt也是基于运算符优先级,他基于每个双目操作符,在被遍历到的时候:
- 当前运算符优先级比之前的更高,则
cur.left=两个运算符中间的节点 - 当前运算符优先级比之前的更低,则
pre.right=两个运算符中间的节点
还是有点绕是吧给个例子。
上来是数字1,因为不是双目运算符,所以往下走一步,看到加号,加号的优先级是1,比初始的0要高,所以加号的左边挂上节点数字1.
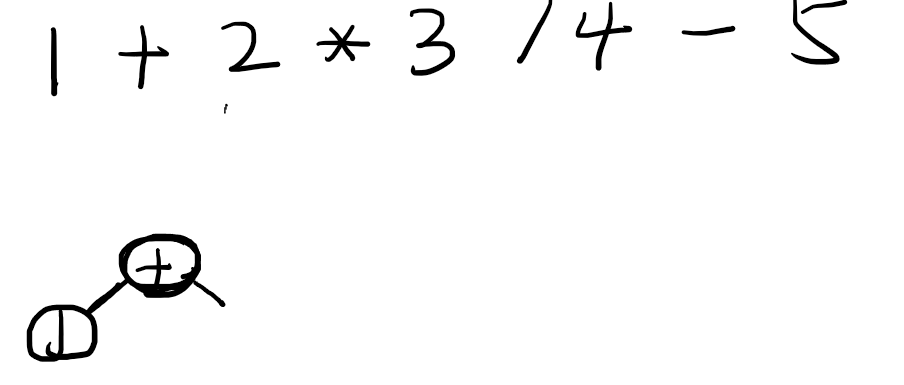
加号的right只能等于parseExpresstion(2[index], 1[+的优先级])进行递归,递归情况和之前一样,遇到了数字节点,然后往下找到双目运算符乘法,
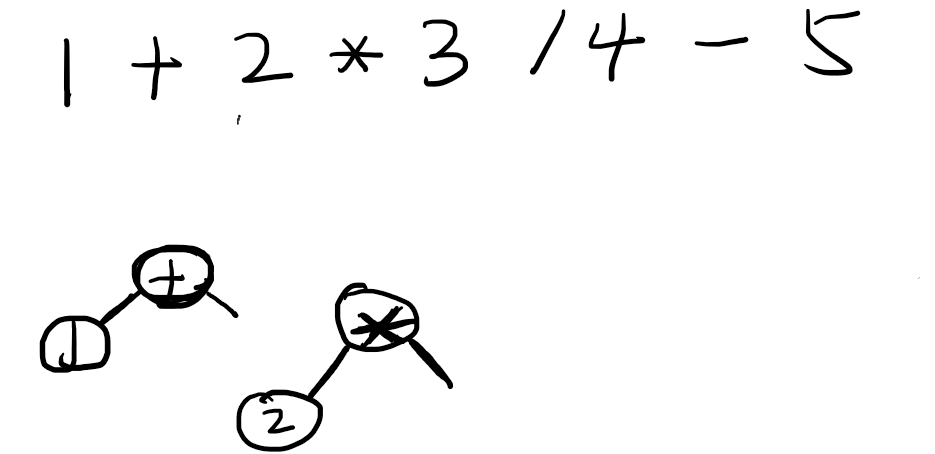
继续递归,到了数字3,然后是触发运算符,但是此时发现除法运算符的优先级是小于等于上下文带过来的乘法运算符的,此时乘法的right节点就等于夹在中间的数字3。
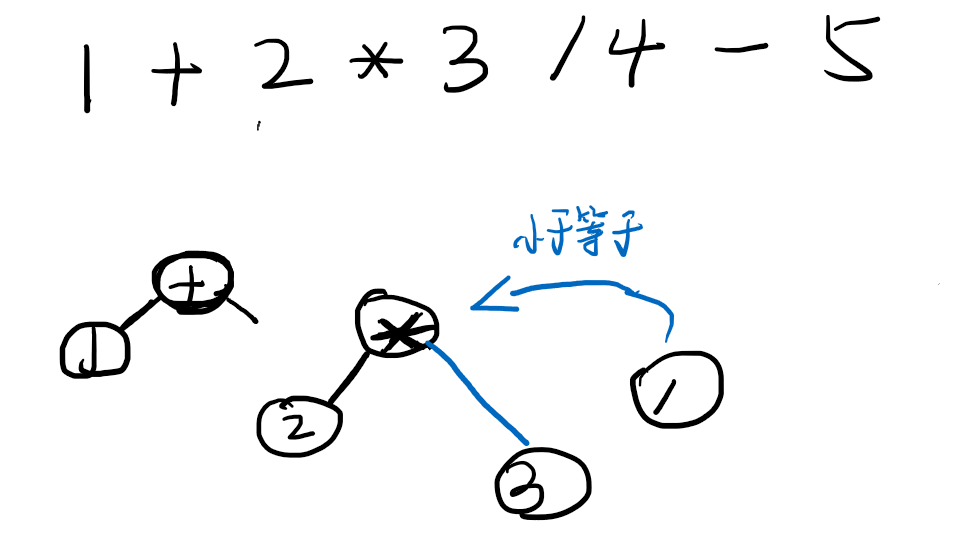
然后二层递归结束了,就到了一层的递归,除法在和加法比较优先级,比加法优先级高,所以/的left是中间的乘法节点,如下。
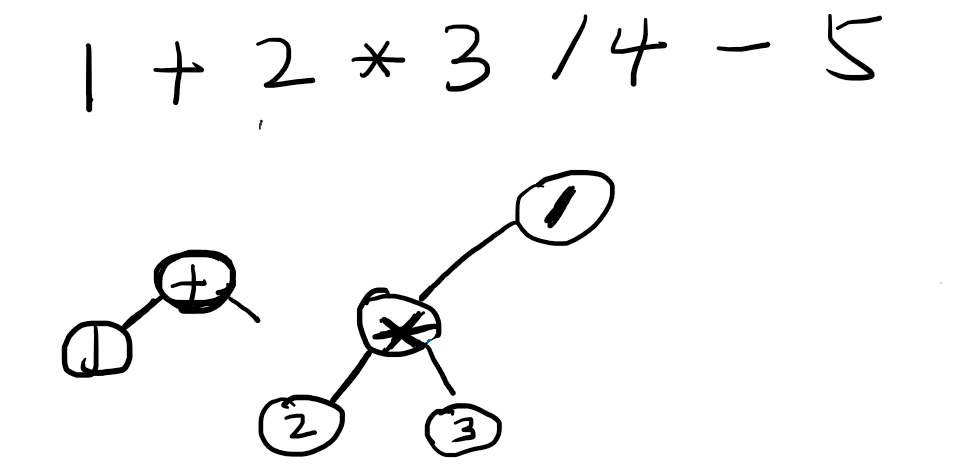
继续,到了减法,减法优先级低于除法,所以除法的right=4;接下来,减法继续和上一层的加法比较。
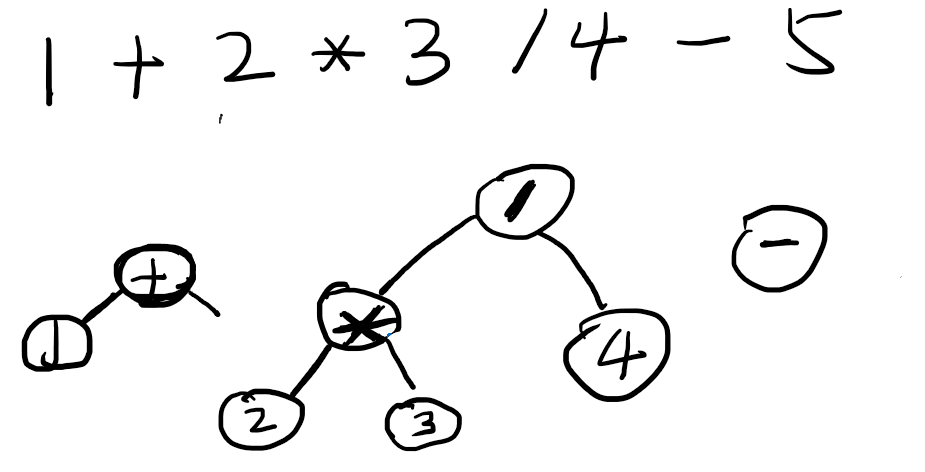
减法和加法同样优先级,但是更靠后,所以加法获胜,加法赢得了自己的right
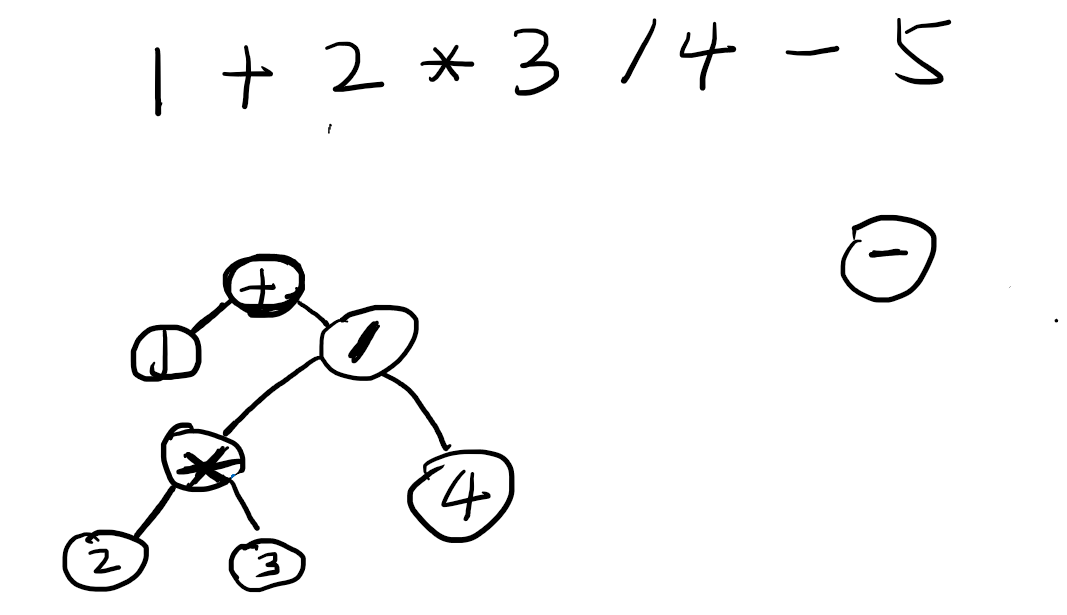
此时递归到了最上层,优先级是初始的0,减法优先级大于0.所以减法拿下了自己的left,继续往下数字5,后面是EOF了,EOF可以认为是0的操作符,减法大于0,所以又赢得了自己的right是5.
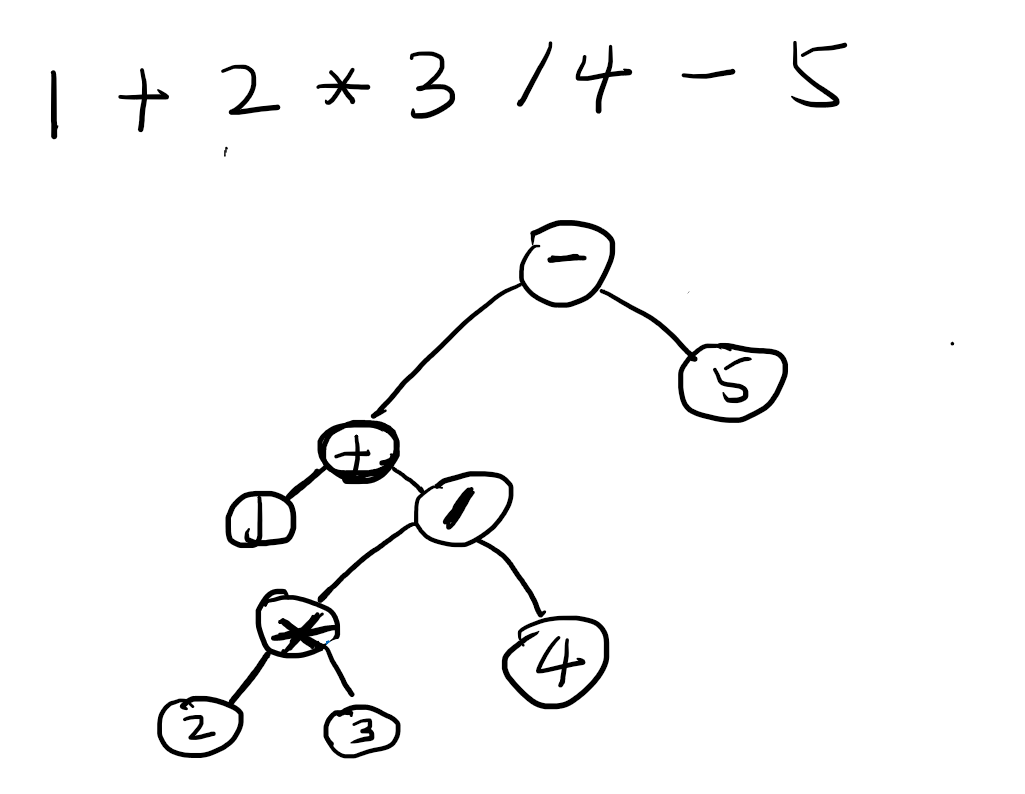
那来实现一下:
// 参数中添加了优先级
import * as LEX from "./lex.mjs";
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode,precedenceMap} from './parser_class_v2.mjs'
export function parseExpression(tokens, start, precedence=0) {
// 因为用到递归,并且因为有递归,所以start这个下标的位置需要用引用类型
// 这样递归更深中的移动,也会在上层改变start的值,所以进入前简单处理下start如果是数字,修改为对象类型
if (start.index === undefined) {
return parseExpression(tokens, {index:start}, precedence);
}
var leftNode = new NumberAstNode(tokens[start.index].value);
while (start.index < tokens.length - 1 && isValidInfixOperator(tokens[start.index + 1])) {
var opNode = new InfixOperatorAstNode(tokens[start.index + 1]);
if (opNode.precedence <= precedence) {
return leftNode;
} else {
opNode.left = leftNode;
start.index += 2;
opNode.right = parseExpression(tokens, start, opNode.precedence);
leftNode = opNode;
}
}
return leftNode;
}
function isValidInfixOperator(token) {
// 在运算符列表中的合法运算符
return precedenceMap[token.value] !== undefined;
}
这里我们需要创建一个新的测试文件,因为test3文件中parseExpression也用了三个参数,但是第三个参数是end位置与这里定义的优先级不一致,这里定义test4,只需要把parseExpression中的end参数去掉.
import * as LEX from "./lex.mjs";
import {VarStatement, ReturnStatement, BlockStatement, ExpressionStatement} from './parser_class_v2.mjs'
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode} from './parser_class_v2.mjs'
import {parseExpression} from './parser_parse_exp_v4.mjs'
// import {parseExpression} from './parser_parse_exp_v5.mjs'
// import {parseExpression} from './parser_parse_exp_v6.mjs'
function parse(tokens) {
function parseVarStatement() {
assert(tokens[i++].type === LEX.VAR, "VarStatement should start with var");
assert(tokens[i].type === LEX.IDENTIFIER, "IDENTIFIER should follow var");
var name = new IdentifierAstNode(tokens[i++]);
assert(tokens[i++].type === LEX.ASSIGN, "ASSIGN should follow IDENT");
for (var x = i; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var value = parseExpression(tokens, x);
return new VarStatement(name, value);
}
}
}
function parseReturnStatement() {
assert(tokens[i].type === LEX.RETURN, "ReturnStatement should start with return");
for (var x = i + 1; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var value = parseExpression(tokens, x);
return new ReturnStatement(value);
}
}
}
function parseExpressionStatement() {
for (var x = i; i < tokens.length; i++) {
if (tokens[i].type === LEX.SEMICOLON || tokens[i].type === LEX.EOF) {
var expression = parseExpression(tokens, x);
return new ExpressionStatement(expression);
}
}
}
function parseBlockStatement() {
assert(tokens[i].type === LEX.LBRACE, "ReturnStatement should start with LBRACE");
var statements = parse(tokens.slice(i + 1));
// !! 需要自己给i赋值新的结束位置,因为递归是值传递i的值
var count = 1;
for (i = i + 1; i < tokens.length; i++) {
if (tokens[i].type === LEX.LBRACE) count++;
else if (tokens[i].type === LEX.RBRACE) count--;
if (count == 0) {
break;
}
}
return new BlockStatement(statements);
}
var statements = [];
for (var i = 0; i < tokens.length; i++) {
var token = tokens[i];
var statement = null;
if (token.type === LEX.SEMICOLON) {
continue;
} else if (token.type === LEX.EOF || token.type === LEX.RBRACE) {
break;
} else if (token.type === LEX.VAR) {
statement = parseVarStatement(tokens, i);
} else if (token.type === LEX.RETURN) {
statement = parseReturnStatement(tokens, i);
} else if (token.type === LEX.LBRACE){
statement = parseBlockStatement(tokens, i);
} else {
statement = parseExpressionStatement(tokens, i);
}
statements.push(statement);
}
return statements;
}
function assert(condition, msg) {
if (!condition) {
if (msg) throw new Error(msg);
throw new Error("assert failed");
}
}
var code = `var a = 1 + 2 * 3 / 4 - 5;`;
var tokens = LEX.lex(code);
var statements = parse(tokens)
for (var i = 0; i < statements.length; i++) {
console.log(statements[i].toString());
}
这个parser_parse_exp_v4代码行数不多,甚至比之前任何一种解法代码都少得多,但是因为有循环和递归,并且dfs中是有返回值的情况是比较难理解的,我们可以把上述代码改为无返回值的dfs形式,这种比较好理解一点:
import * as LEX from "./lex.mjs";
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode,precedenceMap} from './parser_class_v2.mjs'
export function parseExpression(tokens, start, preNode) {
// 第一次调用的时候,preNode也是不传的,我们自己构造一个哨兵节点
if (start.index === undefined) {
preNode = new InfixOperatorAstNode(''); preNode.precedence = 0;
parseExpression(tokens, {index:start},preNode)
return preNode.right;
}
// 我们把变量名改为mid,每次循环中的处理,就是为了决定mid这个中间元素的归属
// 如果当前操作符优先级比前一个要高,则归当前opNode的left
// 否则,mid归前一个的right,前一个咋来的呢,是递归传进来的preNode
var mid = new NumberAstNode(tokens[start.index].value);
var precedence = preNode.precedence;
// start数值参数换成对象的原因是,下面的递归会改动这个指针.
// 而指针的移动是不可逆的,所以要传指针,而不是传值。
while (start.index < tokens.length - 1 && isValidInfixOperator(tokens[start.index + 1])) {
var opNode = new InfixOperatorAstNode(tokens[start.index + 1]);
if (opNode.precedence <= precedence) {
preNode.right = mid; // pre赢得mid,pre左右都填充了
return;
} else {
opNode.left = mid; // opNode赢得mid
start.index += 2; // 指针往后移动2个(每次移动2个),一个数字一个符号
parseExpression(tokens, start, opNode); // opNode作为preNode,指针往后移动
mid = opNode; // opNode的right在递归中填充完毕,此时他作为下一任mid
}
}
preNode.right = mid;
}
function isValidInfixOperator(token) {
// 在运算符列表中的合法运算符
return precedenceMap[token.value] !== undefined;
}
改成上面的无返回值形式,配合代码的注释更好理解了。
2.1.4 栈版本的Pratt算法
但因为有递归还是没有很平面化,我们用栈的方式能更好的理解这个算法。如下图,我们每次遍历两个元素,一个是中间元素mid,一个是操作符。这里的中间元素一定是数字,或者left,right都已填充的操作符节点。while循环,每次只需要准备栈顶元素、mid中间元素、当前操作符元素,栈顶和当前优先级pk,决定mid是归谁。
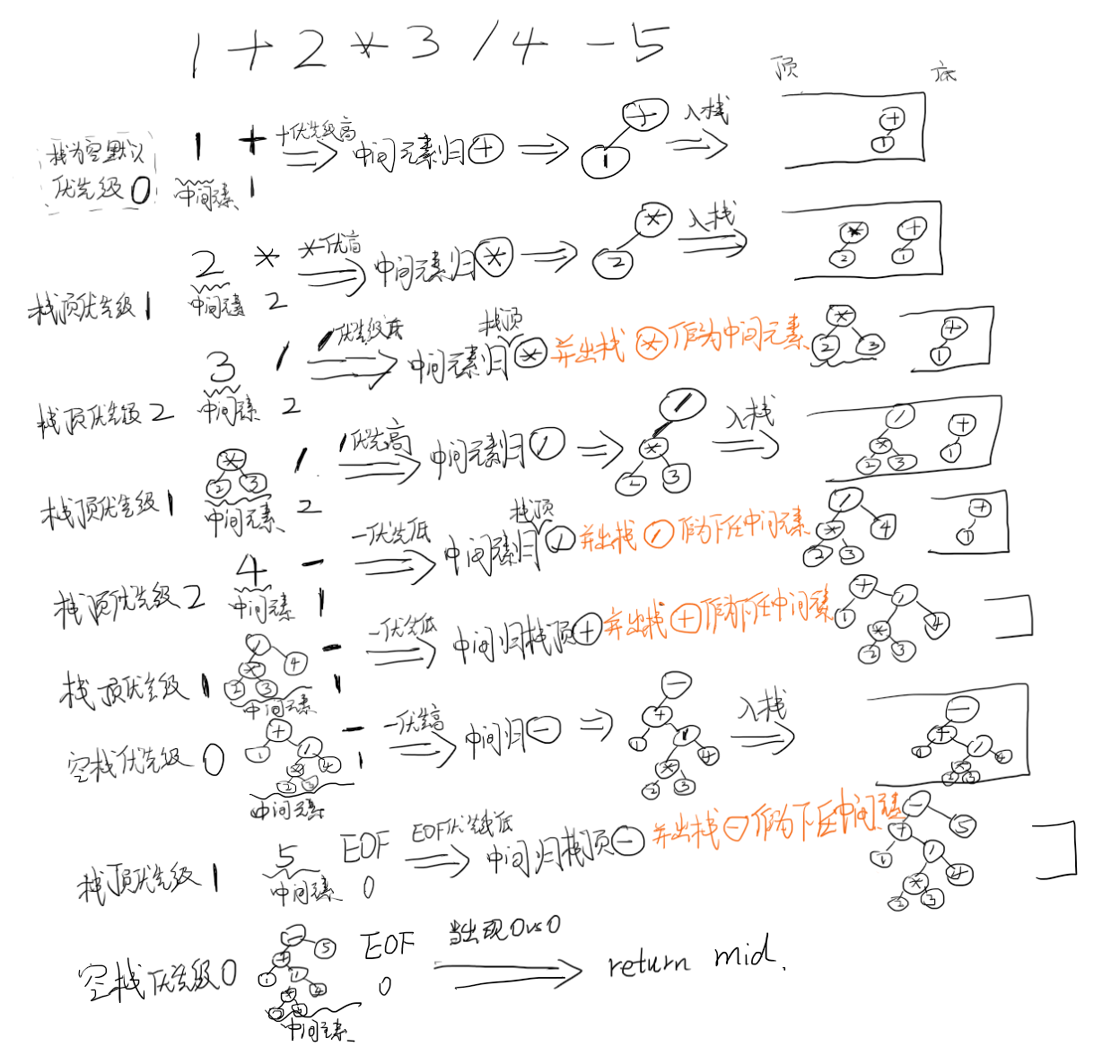
每次循环要做的事情,就是将栈顶元素(一定是right为空的操作符节点)和当前操作符进行优先级PK,优先级更高的获得中间元素,如果是当前操作符赢了,那么要将中间元素挂在自己左边(因为位置上就是在自己左边),否则中间元素挂在栈顶元素的右边。如果是后者的话,栈顶元素的right就填充好了,此时他不能再留在栈中了,就弹出来作为下一任中间元素,继续循环。下一次循环中,当前遍历的指针不动,只是中间元素换成了弹出的栈顶元素,而当前栈顶元素也要换人。而循环结束的条件就是,左边是空栈(前面没有未完成的操作符),右边是EOF(后面也没有未完成的操作符),直接返回mid(中间的就是结果了)。该版本的代码在24.11/parser_test5.mjs:
import * as LEX from "./lex.mjs";
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode,precedenceMap} from './parser_class_v2.mjs'
export function parseExpression(tokens, start) {
var stack = [];
var i = start, mid = null;
while (true) {
// 每个循环,准备好栈顶优先级、中间元素、当前操作符
var stackTopPrecedence = stack.length == 0? 0: stack[stack.length - 1].precedence;
mid = mid == null ? new NumberAstNode(tokens[i++].value) : mid;
var opNode = getEofOrInfixNode(tokens, i);
// 结束循环的条件
if (opNode.precedence == 0 && stackTopPrecedence == 0)return mid;
// 栈顶操作符赢得mid:弹出栈顶,填充right,并作为新的mid; NULL是EOF是最低优先级
if (opNode.precedence <= stackTopPrecedence) {
var top = stack.pop();
top.right = mid;
mid = top;
}
// 当前操作符赢得mid:塞入栈中,继续向后走
else {
opNode.left = mid;
stack.push(opNode);
i++;
mid = null; // 往后走取新的mid
}
}
}
function getEofOrInfixNode(tokens, index) {
var eof = new InfixOperatorAstNode(new LEX.Token(LEX.EOF, 'EOF'));
if (index >= tokens.length) return eof
var token = tokens[index];
if (precedenceMap[token.value] == null) {
return eof;
}
return new InfixOperatorAstNode(tokens[index]);
}
这样的单层循环,理解起来是不是比递归要简单多了,其实本质上是一样的,只是用栈模拟了递归的过程,这样对于pratt的解析,我们用了多种代码的形式,有了非常深刻的理解。
2.2 其他表达式
上面花了大量篇幅来讲四则运算的语法分析,而实际上表达式除了四则运算符,还有其他的很多形式,正如上面提到的,我们还需要整理代码来适配:
- 数字、字符串、布尔值、null、变量,这些单个值就是表达式,比如
1、"hello"、true、null、a等。 - 前缀操作符 + 另一个表达式形成新的表达式,例如
-1、!true等。 - 另一个表达式 + 后缀操作符,例如
a++、a--等。 - 二元操作符 + 左右两个表达式,例如
1 + 2、a > b、x = 1等。 - 函数调用,例如
add(a, b),注意函数的每个参数也需要是表达式。 - 括号(组group)包住子表达式,例如
(1 + 2)。 - 函数声明,在很多解释型语言中,函数声明也是表达式该表达式返回值就是函数本身,例如
var add = function(a, b) { return a + b; }。
2.2.1 字面量类型
对于第一种字面量类型的,我们判断token的类型即可,四则运算代码中都是数字的Node,只需要判断token类型转换成对应的NumberNode,StringNode,BooleanNode,NullNode,IdentifierNode即可;以下为各种AstNode代码,这里把之前其实一直也没再使用的full属性删掉了,代码更简洁。
// 前面部分与v2是一样的,这里省略
// 数字字面量
export class NumberAstNode extends AstNode {
constructor(token) {
super();
this.token = token;
}
toString() {
return this.token.value;
}
}
// 变量名/函数名字面量
export class IdentifierAstNode extends AstNode {
constructor(token) {
super();
this.token = token;
}
toString() {
return this.token.value;
}
}
// null字面量
export class NullAstNode extends AstNode {
toString() {
return "null";
}
}
// 字符串字面量
export class StringAstNode extends AstNode {
constructor(token) {
super();
this.token = token;
}
toString() {
return this.token.value;
}
}
// boolean字面量
export class BooleanAstNode extends AstNode {
constructor(token) {
super();
this.token = token;
}
toString() {
return this.token.value;
}
}
// 中缀操作符节点
export class InfixOperatorAstNode extends AstNode {
constructor(token) {
super();
this.op = token;
this.left = null;
this.right = null;
this.precedence = precedenceMap[token.value];
}
toString() {
return `(${this.left.toString()} ${this.op.value} ${this.right.toString()})`;
}
}
// 前缀操作符
export class PrefixOperatorAstNode extends AstNode {
constructor(token, right) {
super(false);
this.op = token;
this.right = right;
}
toString() {
return `(${this.op.value} ${this.right.toString()})`;
}
}
// 后缀操作符
export class PostfixOperatorAstNode extends AstNode {
constructor(token, left) {
super(false);
this.op = token;
this.left = left;
}
toString() {
return `(${this.left.toString()} ${this.op.value})`;
}
}
// 函数声明
class FunctionDeclarationAstNode extends AstNode {
constructor(params, body) {
super();
this.params = params;
this.body = body;
}
toString() {
return `function(${this.params.join(',')})${this.body.toString()}`;
}
}
// 函数调用
export class FunctionCallAstNode extends AstNode {
constructor(name, args) {
super();
this.name = name;
this.args = args; // args是ast数组
}
toString() {
return `${this.name.toString()}(${this.args.map(it=>it.toString()).join(',')})`
}
}
// 分组节点
export class GroupAstNode extends AstNode {
constructor(exp) {
super();
this.exp = exp;
}
toString() {
// 因为小括号已经在运算符的toString中使用了,这里为了更好的凸显使用中文中括号
return `【${this.exp.toString()}】`
}
}
// 等等,如果还要支持其他语法特性,需要增加其他节点。
2.2.2 单元操作符
前缀运算符有++、--、+、-、!、~。同一个符号出现时可能有多重身份,例如-可以是前缀,也可能是中缀。这就需要一些额外的判断,如果前一个token是括号三兄弟([{或者位于开始位置或者是其他中缀运算符,那么这个位置-就是前缀运算符,否则就是中缀运算符。而对于++这种可能是前缀,也可能是后缀的运算符,也可按照上述判断是否是前缀,如果不是前缀,就是后缀运算符。以上面基于栈的pratt算法为基础进行改造:
- mid = mid == null ? new NumberAstNode(tokens[i++].value) : mid;
+ mid = mid == null ? nextUnaryNode() : mid;
...
+ // 这个函数的定义放到parseExpression函数里面
+ function nextUnaryNode() {
+ var token = tokens[i];
+ var node = null;
+ switch (token.type) {
+ case LEX.NUMBER:
+ node = new NumberAstNode(tokens[i++]);
+ break;
+ case LEX.STRING:
+ node = new StringAstNode(tokens[i++]);
+ break;
+ case LEX.BOOLEAN:
+ node = new BooleanAstNode(tokens[i++]);
+ break;
+ case LEX.NULL:
+ node = new NullAstNode(tokens[i++]);
+ break;
+ // 遇到前缀运算符
+ case LEX.PLUS:
+ case LEX.MINUS:
+ case LEX.INCREMENT:
+ case LEX.DECREMENT:
+ case LEX.NOT:
+ case LEX.BIT_NOT:
+ // 前缀后面递归解析一元节点(前缀后面一定是个一元节点)
+ // 并且前缀操作符都是右结合的,所以递归结合(递归=栈=后来的先结合)
+ node = new PrefixOperatorAstNode(tokens[i++], nextUnaryNode());
+ break;
+ default:
+ throw new Error('unexpected token in getNode: ' + token.type);
+ }
+ // 后缀,都是左结合的,所以遇到就合并
+ while (tokens[i].type == LEX.INCREMENT || tokens[i].type == LEX.DECREMENT) {
+ node = new PostfixOperatorAstNode(tokens[i++], node);
+ }
+ return node;
+ }
对应的测试代码在24.11/parser_test5.mjs
2.2.3 分组类型
(1 + 2) * 3这里的小括号就是分组,需要在nextUnaryNode函数中添加LPAREN左括号的识别,识别到之后就则需要递归进行表达式的解析,代码类似这样:
function nextUnaryNode() {
//...
case LEX.LPAREN:
node = new GroupAstNode(parseExpression(tokens, i + 1));
break;
//...
}
但是这里有个问题,在调用parseExpression函数结束的时候,i实际上没有任何变化(1 + 2)*3的例子中i位于左括号,而递归parseExpression运行结束后,i还是0,这样就死循环了,问题其实出在parseExression函数的start是值传递的,导致运行结束后,上层的i值是没有变的。有三种方式可以让上层感知变量的变化:
- 1 上面用过的
start = {index: i},用对象,即引用传递 - 2 用返回值,在返回值中带一个属性
endPos,递归调用结束后,令i = res.endPos - 3 用更大范围的全局变量,比如把
parseExpressionparseXXX....所有的方法都放到一个class中,i作为class一个属性,这样就成为一个所有函数看来的全局变量了,这也是一种面向对象的思想,状态i作为对象的属性,是非常推荐的一种代码写法,其实我们应该在一开始就用对象来封装的,但是上来用对象封装很多人会觉得不适,好像被强加了一些代码风格,会质疑为什么要用对象,不用可不可以,所以我们从文章开始到现在,都没有使用对象的方式,在这个过程中大家能深刻的感受到了全局变量i传递的时候的不方便,甚至我们被逼的在函数中定义函数,来利用上一级函数的全局变量i,但是到这里我们终于发现,原来用class封装的方式可以更好的维护代码了,我们就可以带着之前的理解来迎接class形式的代码了。 - 4 就
js可以传入闭包,例如parseExpression(tokens, i + 1, (endPos)=> i = endPos),然后parseExpression(tokens, start, endCallBack=()=>{})的return的这一行改成endCallBack(i); return mid;,闭包本质上是传入了一个含有外部i引用类型。所以其实和方法1是一个道理,没什么特殊的
我们使用方法3,然后将之前的所有的方法,都平级放到class Parser中,全量代码参考24.11/parser_test6.mjs,这里我们把Parser类列出:
import * as LEX from "./lex.mjs";
import {VarStatement, ReturnStatement, BlockStatement, ExpressionStatement, precedenceMap} from './parser_class_v3.mjs'
import {AstNode, IdentifierAstNode, NumberAstNode, InfixOperatorAstNode, PrefixOperatorAstNode, PostfixOperatorAstNode, GroupAstNode} from './parser_class_v3.mjs'
class Parser {
constructor(tokens) {
this.tokens = tokens;
this.cursor = 0;
}
parse() {
var tokens = this.tokens;
var statements = [];
for (;;) {
var token = tokens[this.cursor];
var statement = null;
if (token.type === LEX.SEMICOLON) {
this.cursor++;
continue;
} else if (token.type === LEX.EOF || token.type === LEX.RBRACE) {
break;
} if (token.type === LEX.VAR) {
statement = this.parseVarStatement();
} else if (token.type === LEX.RETURN) {
statement = this.parseReturnStatement();
} else if (token.type === LEX.LBRACE) {
statement = this.parseBlockStatement();
} else {
statement = this.parseExpressionStatement();
}
statements.push(statement);
}
return statements;
}
parseVarStatement() {
var tokens = this.tokens;
assert(tokens[this.cursor++].type === LEX.VAR, "VarStatement should start with var");
assert(tokens[this.cursor].type === LEX.IDENTIFIER, "IDENTIFIER should follow var");
var name = new IdentifierAstNode(tokens[this.cursor++]);
assert(tokens[this.cursor++].type === LEX.ASSIGN, "ASSIGN should follow IDENT");
for (var x = this.cursor; this.cursor < tokens.length; this.cursor++) {
if (tokens[this.cursor].type === LEX.SEMICOLON || tokens[this.cursor].type === LEX.EOF) {
var value = this.parseExpression(tokens, x);
return new VarStatement(name, value);
}
}
}
parseVarStatement() {
var tokens = this.tokens;
assert (tokens[this.cursor].type === LEX.VAR);
assert (tokens[this.cursor + 1].type === LEX.IDENTIFIER);
assert (tokens[this.cursor + 2].type === LEX.ASSIGN);
var name = new IdentifierAstNode(tokens[this.cursor + 1]);
this.cursor = this.cursor + 3
var value = this.parseExpression();
assert(tokens[this.cursor].type === LEX.SEMICOLON || tokens[this.cursor].type == LEX.EOF);
this.cursor ++;
return new VarStatement(name, value);
}
parseReturnStatement() {
var tokens = this.tokens;
assert(tokens[this.cursor++].type === LEX.RETURN, "ReturnStatement should start with return");
var value = this.parseExpression();
assert(tokens[this.cursor].type === LEX.SEMICOLON || tokens[this.cursor].type == LEX.EOF);
this.cursor ++;
return new ReturnStatement(value);
}
parseExpressionStatement() {
var tokens = this.tokens;
var expression = this.parseExpression();
assert(tokens[this.cursor].type === LEX.SEMICOLON || tokens[this.cursor].type == LEX.EOF);
this.cursor ++;
return new ExpressionStatement(expression);
}
parseBlockStatement() {
var tokens = this.tokens;
assert(tokens[this.cursor++].type === LEX.LBRACE, "brace not open for block statement")
var result = new BlockStatement(this.parse());
assert(tokens[this.cursor++].type === LEX.RBRACE, "brace not close for block statement");
return result
}
parseExpression() {
var tokens = this.tokens;
var stack = [];
var mid = null;
while (true) {
var stackTopPrecedence = stack.length == 0? 0: stack[stack.length - 1].precedence;
mid = mid == null ? this.nextUnaryNode() : mid;
var opNode = this.getEofOrInfixNode(tokens, this.cursor);
if (opNode.precedence == 0 && stackTopPrecedence == 0)return mid;
if (opNode.precedence <= stackTopPrecedence) {
var top = stack.pop();
top.right = mid;
mid = top;
}
else {
opNode.left = mid;
stack.push(opNode);
this.cursor++;
mid = null;
}
}
}
nextUnaryNode() {
var tokens = this.tokens;
var node = null;
switch (tokens[this.cursor].type) {
case LEX.NUMBER:
node = new NumberAstNode(tokens[this.cursor++]);
break;
case LEX.STRING:
node = new StringAstNode(tokens[this.cursor++]);
break;
case LEX.BOOLEAN:
node = new BooleanAstNode(tokens[this.cursor++]);
break;
case LEX.NULL:
node = new NullAstNode(tokens[this.cursor++]);
break;
case LEX.IDENTIFIER:
node = new IdentifierAstNode(tokens[this.cursor++]);
break;
// 遇到前缀运算符
case LEX.PLUS:
case LEX.MINUS:
case LEX.INCREMENT:
case LEX.DECREMENT:
case LEX.NOT:
case LEX.BIT_NOT:
// 前缀后面递归解析一元节点(前缀后面一定是个一元节点)
// 并且前缀操作符都是右结合的,所以可以直接递归。
node = new PrefixOperatorAstNode(tokens[this.cursor++], this.nextUnaryNode());
break;
// 分组
case LEX.LPAREN:
// 递归解析(后面的即可,因为遇到)的时候,parseExpression无法识别,就会结束解析
this.cursor++;
// GroupAstNode其实可有可无
node = new GroupAstNode(this.parseExpression());
assert(tokens[this.cursor++].type == LEX.RPAREN, "group not closed");
break;
default:
throw new Error('unexpected token in nextUnary: ' + tokens[this.cursor].type);
}
// 后缀操作符,后缀操作符都是左结合的,并且后缀操作符的优先级比前缀都要高
while (tokens[this.cursor].type == LEX.INCREMENT || tokens[this.cursor].type == LEX.DECREMENT) {
node = new PostfixOperatorAstNode(tokens[this.cursor++], node);
}
return node;
}
getEofOrInfixNode(tokens, index) {
var eof = new InfixOperatorAstNode(new LEX.Token(LEX.EOF, 'EOF'));
if (index >= tokens.length) return eof
var token = tokens[index];
if (precedenceMap[token.value] == null) {
return eof;
}
return new InfixOperatorAstNode(tokens[index]);
}
}
function assert(condition) {
if (!condition) {
throw new Error("assert failed");
}
}
var code = `var a = 1 * (2 - 3);
return 1 * 3 - b;
{a * 3 - 1;}
`;
var tokens = LEX.lex(code);
var statements = new Parser(tokens).parse()
for (var i = 0; i < statements.length; i++) {
console.log(statements[i].toString());
}
另外有了全局的地方记录cursor的值,我们也可以修改一元(前缀/后缀)操作符的代码了,前缀操作符目前是node = new PrefixOperatorAstNode(tokens[this.cursor++], this.nextUnaryNode());来实现的,其实递归的this.nextUnaryNode()也可以改成递归parseExpression()。即我们对前缀操作符和二元操作符一视同仁,只不过前缀操作符left节点是已经填充好的。如下也是一种思路(以下几种变体的思路,如果不想了解也可以不看)
//....
// 补充下前后缀运算符优先级
const prefixPrecedenceMap = {
'-': 100,
'!': 100,
'~': 100,
'+': 100,
'++': 100,
'--': 100
}
...
// 遇到前缀运算符
case LEX.PLUS:
case LEX.MINUS:
case LEX.INCREMENT:
case LEX.DECREMENT:
case LEX.NOT:
case LEX.BIT_NOT:
// 使用parseExpression函数递归,但是要传递当前符号的优先级
node = new PrefixOperatorAstNode(tokens[this.cursor], this.parseExpression(prefixPrecedenceMap[tokens[this.cursor++].value]));
break;
// 分组
case LEX.LPAREN:
// 递归解析(后面的即可,因为遇到)的时候,parseExpression无法识别,就会结束解析
this.cursor++;
node = new GroupAstNode(this.parseExpression());
assert(tokens[this.cursor++].type == LEX.RPAREN, "group not closed");
break;
....
// 然后修改parseExpression函数,使其接受一个参数,代表前置符号的优先级
parseExpression(precedence = 0) {
var tokens = this.tokens;
var stack = [];
var mid = null;
while (true) {
// 此时栈为空的时候默认看到的就是上下文传进来的优先级
var stackTopPrecedence = stack.length == 0 ? precedence: stack[stack.length - 1].precedence;
mid = mid == null ? this.nextUnaryNode() : mid;
var opNode = this.getEofOrInfixNode(tokens, this.cursor);
// 结束循环的条件改为,当前操作符优先级<=上下文优先级 并且 栈为空
// 这样首先是能兼容为0的情况,其次前缀操作符优先级是比中缀高的,所以前缀操作符传进来的时候一定是遇到中缀就结束
if (opNode.precedence <= precedence && stackTopPrecedence == precedence) return mid;
if (opNode.precedence <= stackTopPrecedence) {
var top = stack.pop();
top.right = mid;
mid = top;
}
else {
opNode.left = mid;
stack.push(opNode);
this.cursor++;
mid = null;
}
}
}
测试没有问题:

但是我还想再改一下代码,因为在分组和前缀表达式中,都使用了递归调用parseExpression,分组的比较容易接受,因为分组内是一个全新的表达式解析的过程,但是前缀和后缀表达式其实是一种特殊的二元表达式,我们其实可以把前缀和后缀表达式的处理合并到while循环中,代码如下:
pa parseExpression() {
var tokens = this.tokens;
var stack = [];
var mid = null;
while (true) {
var stackTopPrecedence = stack.length == 0? 0: stack[stack.length - 1].precedence;
if (mid == null) {
// 如果是前缀运算符,不需要设置left,直接塞到stack
if (prefixPrecedenceMap[tokens[this.cursor].value]) {
stack.push(new PrefixOperatorAstNode(tokens[this.cursor++]));
continue;
}
mid = this.nextUnaryNode();
}
var opNode = this.getEofOrOperateNode(tokens, this.cursor);
if (opNode.precedence == 0 && stackTopPrecedence == 0)return mid;
if (opNode.op.type === LEX.ASSIGN ? opNode.precedence < stackTopPrecedence : opNode.precedence <= stackTopPrecedence) {
var top = stack.pop();
top.right = mid;
mid = top;
} else {
opNode.left = mid;
// 如果是后缀运算符,不需要设置right直接continue
if (opNode instanceof PostfixOperatorAstNode) {
mid = opNode; this.cursor++;
continue;
}
stack.push(opNode);
if (opNode.op.type != LEX.LPAREN && opNode.op.type != LEX.LBRACKET) this.cursor++;
else opNode.precedence = 999;
mid = null;
}
}
}
nextUnaryNode() {
var tokens = this.tokens;
var node = null;
switch (tokens[this.cursor].type) {
case LEX.NUMBER:
node = new NumberAstNode(tokens[this.cursor++]);
break;
case LEX.STRING:
node = new StringAstNode(tokens[this.cursor++]);
break;
case LEX.TRUE:
case LEX.FALSE:
node = new BooleanAstNode(tokens[this.cursor++]);
break;
case LEX.NULL:
node = new NullAstNode(tokens[this.cursor++]);
break;
case LEX.IDENTIFIER:
node = new IdentifierAstNode(tokens[this.cursor++]);
break;
case LEX.LPAREN:
// 递归解析(后面的即可,因为遇到)的时候,parseExpression无法识别,就会结束解析
this.cursor++;
// GroupAstNode其实可有可无
node = new GroupAstNode(this.parseExpression());
assert(this.tokens[this.cursor++].type == LEX.RPAREN, "group not closed");
break;
case LEX.FUNCTION:
assert(this.tokens[++this.cursor].type == LEX.LPAREN, "function need a lparen");
this.cursor++;
var params = [];
while (tokens[this.cursor].type != LEX.RPAREN) {
assert(this.tokens[this.cursor].type == LEX.IDENTIFIER);
params.push(new IdentifierAstNode(tokens[this.cursor++]));
if (tokens[this.cursor].type == LEX.COMMA) {
this.cursor++;
}
}
this.cursor++;
var body = this.parseBlockStatement();
node = new FunctionDeclarationAstNode(startToken, params, body)
break;
default:
throw new Error('unexpected token in nextUnary: ' + tokens[this.cursor].type);
}
return node;
}
getEofOrOperateNode(tokens, index) {
var eof = new InfixOperatorAstNode(new LEX.Token(LEX.EOF, 'EOF'));
if (index >= tokens.length) return eof
var token = tokens[index];
if (precedenceMap[token.value] != null) {
return new InfixOperatorAstNode(tokens[index]);
}
if (postfixPrecedenceMap[token.value] != null) {
return new PostfixOperatorAstNode(tokens[index]);
}
// 不需要判断前缀运算符,因为在前面已经判断过了
return eof;
}
结果也是符合预期的:
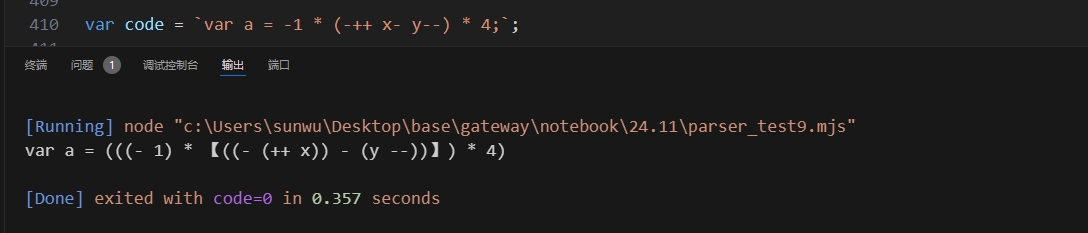
以上两种思路在xxx6_2.mjs和xxx6_3.mjs中有详细代码,都是针对6的简单变体。
2.2.4 中缀运算符
我们上面代码其实都是从中缀运算符为主心骨展开的代码,所以默认就是支持中缀运算符的,不过前面的中缀取值只有四则运算,这里可以丰富下:
export const precedenceMap = {
'EOF': 0,
'=': 10,
'||': 11, '&&': 12, '^': 13,
'==': 14, '!=': 14,
'<': 15, '<=': 15, '>': 15, '>=': 15,
'<<': 16, '>>': 16, '>>>': 16,
'+': 17, '-': 17,
'*': 18, '/': 18, '%': 18,
}
这里面有一个符号比较特殊就是=,他是右结合的,其他都是左结合,结合就是指相同优先级的符号出现2次,先计算左边还是右边,正常的其他符号例如1 + 2 + 3是左结合的(1+2) + 3,而a = b = 1是右侧结合a = (b = 1)。
只需要改parseExpression中一行代码即可:
// 如果是等号,那么是又结合,<= 换成 <
if (opNode.op.type === LEX.ASSIGN ? opNode.precedence < stackTopPrecedence : opNode.precedence <= stackTopPrecedence)//...
2.2.5 函数声明
函数声明,function name(a,b,c){xxx}或者匿名函数赋值给变量var name = function(a,b,c){xxx},因为效果一样,为了简化流程,我们只支持第二种形式,因为这种形式比较简单,函数声明就只是一个表达式,返回值就是函数本身。
在nextUnaryNode函数中,识别function关键字,然后是(0或多个参数),然后是blockStatement即可。
....
case LEX.FUNCTION:
// function后跟左括号
assert(tokens[++this.cursor].type == LEX.LPAREN, "function need a lparen");
this.cursor++;
// 然后是空参数或者多个参数用逗号隔开
var params = [];
while (tokens[this.cursor].type != LEX.RPAREN) {
assert(tokens[this.cursor].type == LEX.IDENTIFIER);
params.push(new IdentifierAstNode(tokens[this.cursor++]));
if (tokens[this.cursor].type == LEX.COMMA) {
this.cursor++;
}
if (tokens[this.cursor].type == LEX.RPAREN) {
this.cursor++;
break;
}
}
// 接下来是个块语句 {xxx}
var body = this.parseBlockStatement();
node = new FunctionDeclarationAstNode(params, body)
break;
....
2.2.6 函数调用
函数调用可以通过函数名add(1,2),也可以通过函数声明的表达式直接调用function(a,b){return a+b;}(1,2),还有可能是一个函数的返回值也是函数,即在前面形式之后调用add(a,b)(a,b),而调用时候的每个入参都是一个表达式。对于函数名调用,则是在nextUnaryNode函数中识别到IDENTIFIER,然后识别到LPAREN,就认为是函数调用,接下来分别识别多个表达式即可,因为遇到逗号这个parseExpression中的符号无法处理,就自动结束了,直到遇到RPAREN才结束。而如果是函数声明也是类似的。
....
case LEX.IDENTIFIER:
node = new IdentifierAstNode(tokens[this.cursor++]);
// 函数调用
while (tokens[this.cursor].type == LEX.LPAREN) {
this.cursor++;
var args = [];
while (tokens[this.cursor].type != LEX.RPAREN) {
args.push(this.parseExpression());
if (tokens[this.cursor].type == LEX.COMMA) {
this.cursor++;
}
}
this.cursor++;
node = new FunctionCallAstNode(node, args);
}
break;
case LEX.FUNCTION:
assert(tokens[++this.cursor].type == LEX.LPAREN, "function need a lparen");
this.cursor++;
var params = [];
while (tokens[this.cursor].type != LEX.RPAREN) {
assert(tokens[this.cursor].type == LEX.IDENTIFIER);
params.push(new IdentifierAstNode(tokens[this.cursor++]));
if (tokens[this.cursor].type == LEX.COMMA) {
this.cursor++;
}
}
this.cursor++;
var body = this.parseBlockStatement();
node = new FunctionDeclarationAstNode(params, body)
// 函数声明直接调用,与变量的代码一模一样
while (tokens[this.cursor].type == LEX.LPAREN) {
this.cursor++;
var args = [];
while (tokens[this.cursor].type != LEX.RPAREN) {
args.push(this.parseExpression());
if (tokens[this.cursor].type == LEX.COMMA) {
this.cursor++;
}
}
this.cursor++;
node = new FunctionCallAstNode(node, args);
}
break;
....
补齐后的全量代码在24.11/parser_test8.mjs。
3 补齐控制流语句
我们上面一共有四种语句VarStatement ReturnStatement BlockStatement和ExpressionStatement,还缺了控制流语句,包括IfStatement ForStatement BreakStatement ContinueStatement,其中for可以替换掉while,所以我们就不实现后者,并且if else的嵌套可以实现if() else if(),所以我们也不实现else if语法了,另外switch也可以被if平替,所以也不实现switch语法。
3.1 IfStatement
if语句有两种形式:if(condition){xxx},if(condition){xxx}else{yyy},我们要做的就是parse函数中识别if关键字,然后parseIfStatement即可。后者是主要的逻辑,为识别(然后parseExpression得到condition,最后是一个块语句。
export class IfStatement extends Statement {
constructor(condition, ifBody, elseBody) {
super("IF");
this.condition = condition;
this.ifBody = ifBody;
this.elseBody = elseBody;
}
toString() {
return `if ${this.condition.toString()} ${this.ifBody.toString()} ${this.elseBody ? `else ${this.elseBody.toString()}` : ""}
`
}
}
parseIfStatement() {
var tokens = this.tokens;
assert(tokens[this.cursor++].type == LEX.IF, "if statement need a if"); // if
assert(tokens[this.cursor++].type == LEX.LPAREN, "if statement need a LPAREN follow if"); // (
var condition = this.parseExpression(); // condition
assert(tokens[this.cursor++].type == LEX.RPAREN, "if statement need a RPAREN follow condition");// )
var ifBody = this.parseBlockStatement(); // {xxx}
if (tokens[this.cursor].type == LEX.ELSE) {
this.cursor++; // else
var elseBody = this.parseBlockStatement(); // {yyy}
}
return new IfStatement(condition, ifBody, elseBody);
}
结果服务预期,因为改动很小就直接在之前的test8文件中直接修改了
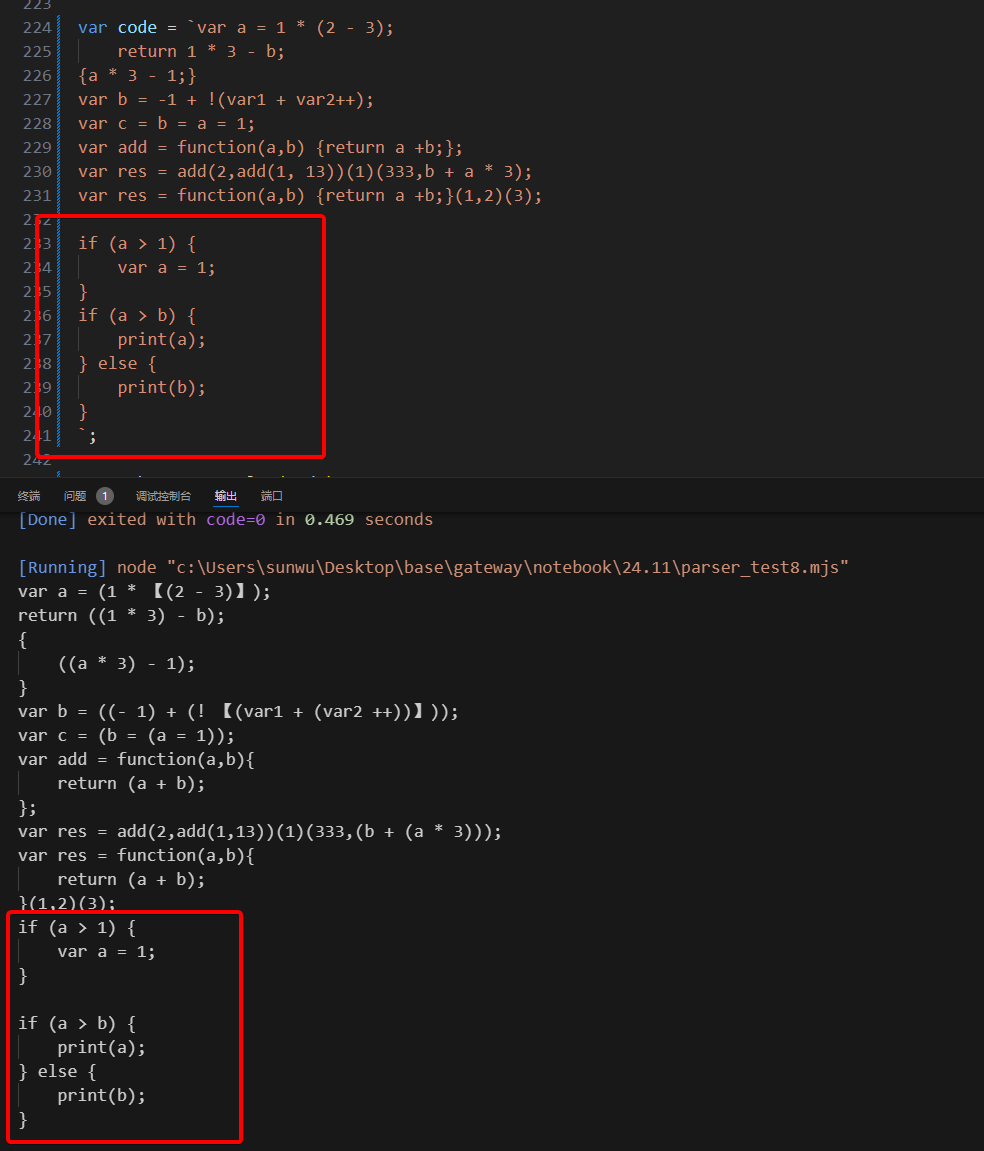
3.2 ForStatement
for语句的语法为:for(init;condition;step){xxx},其中init step condition均可以省略,所以parseForStatement中识别for关键字,即运行parseForStatement函数。主要逻辑在该函数中,主要是识别for之后是(,然后调用parse函数识别期望返回一个长度为3的Statement数组,分别对应init condition step,注意这里要在parse函数中加上,遇到)就停止识别,直接返回。
但是parse其实会报错,因为并不能返回三个语句,第三个语句step后面不是分号而是),所以要么修改parseExpressionStatement,遇到)也返回,要么也可以新增一个parseStatement为解析下一个语句,如下:
class ForStatement extends Statement {
constructor(init, condition, step, body) {
super();
this.init = init;
this.condition = condition;
this.step = step;
this.body = body;
}
}
class BreakStatement extends Statement {}
class ContinueStatement extends Statement {}
parseForStatement() {
var tokens = this.tokens;
assert(tokens[this.cursor++].type == LEX.FOR, "for statement need a for");
assert(tokens[this.cursor++].type == LEX.LPAREN, "for statement need a LPAREN follow for");
var init = this.parseStatement();
assert(tokens[this.cursor-1].type == LEX.SEMICOLON, "for statement error need a SEMICOLON after init");
var condition = this.parseStatement();
assert(tokens[this.cursor-1].type == LEX.SEMICOLON, "for statement error need a SEMICOLON after condition");
var step = this.parseExpression();
assert(tokens[this.cursor++].type == LEX.RPAREN, "for statement need a RPAREN follow condition");
var body = this.parseBlockStatement();
return new ForStatement(init, condition, step, body);
}
parse() {
var statements = [];
for (;;) {
var item = this.parseStatement();
if (item == null) break;
if (item instanceof EmptyStatement) {
continue;
}
statements.push(item);
}
return statements;
}
parseStatement() {
var token = tokens[this.cursor];
if (token.type === LEX.SEMICOLON) {
this.cursor++;
return new EmptyStatement();
} else if (token.type === LEX.EOF || token.type === LEX.RBRACE || token.type === LEX.RPAREN) {
return null;
} if (token.type === LEX.VAR) {
return this.parseVarStatement();
} else if (token.type === LEX.RETURN) {
return this.parseReturnStatement();
} else if (token.type === LEX.LBRACE) {
return this.parseBlockStatement();
} else if (token.type === LEX.IF) {
return this.parseIfStatement();
} else if (token.type === LEX.FOR) {
return this.parseForStatement();
} else if (token.type === LEX.BREAK) {
return new BreakStatement(tokens[this.cursor++]);
} else if (token.type === LEX.CONTINUE) {
return new ContinueStatement(tokens[this.cursor++]);
} else {
return this.parseExpressionStatement();
}
}
在有了强大的parse和parseExpression函数加持下,是不是if和for语句的解析都变简单了。
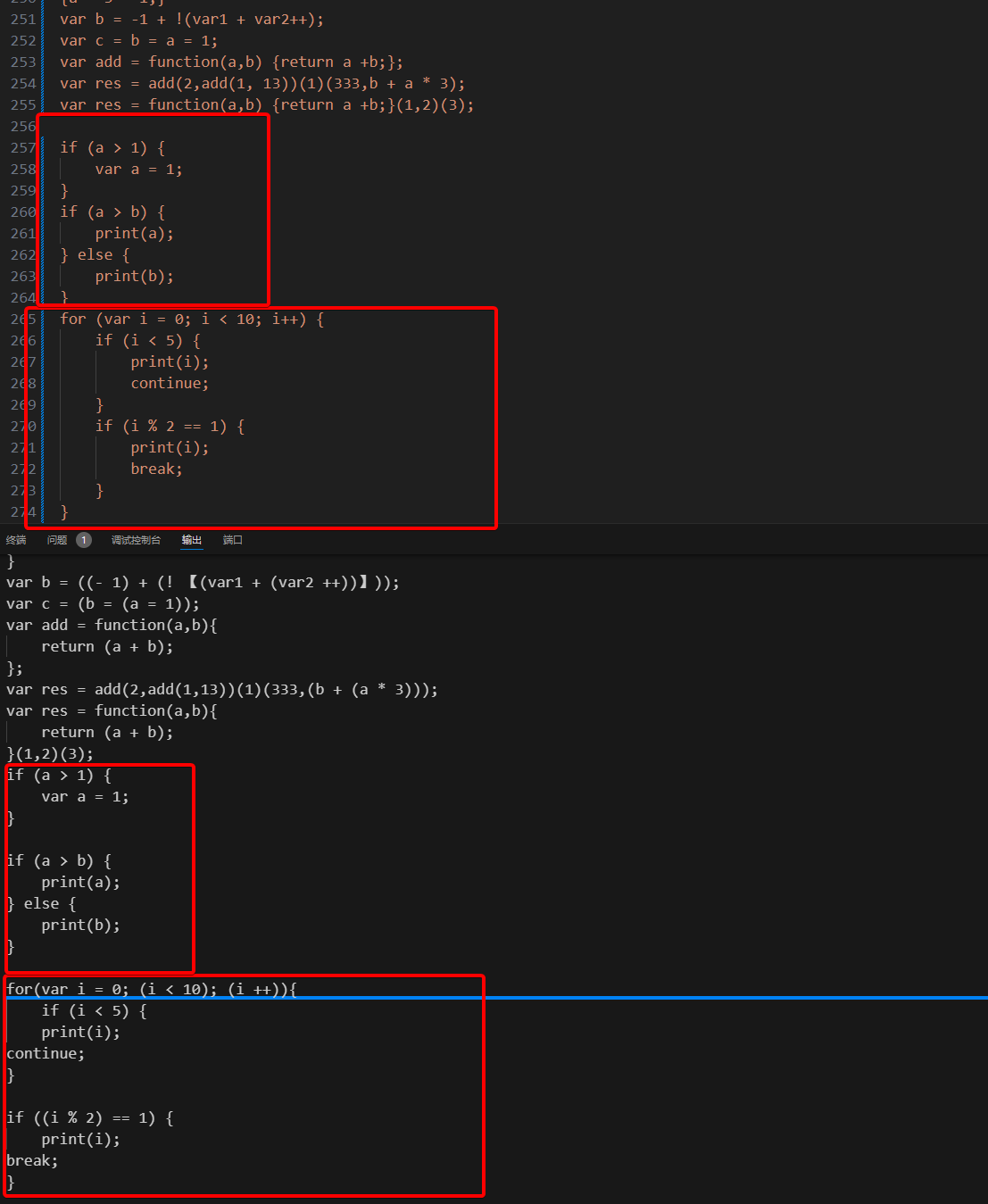
上面代码和测试在parser_test9.mjs文件中。
4 小结
我们将上面代码重新整理,增加了面向对象特性:
- 新增了
.操作符用于new Person().age对象属性获取 - 新增了
(操作符来表示函数调用,上面是直接判断Identifier之后有(,就是函数调用,但是实际是一种简化,因为函数可以作为其他函数的返回值,也可能是对象的属性new Person().getAge(),所以单独把(作为函数调用操作符更合理。 - 新增了
[操作符来表示数组或对象索引,arr[1]person["age"]等。
最终的版本放到了一个新的repo中https://github.com/sunwu51/mocha的parser/parser.js,上一节语法分析则对应lexer/lexer.js,当然语法分析的代码行数要比词法分析多一些,但是整体是重复代码较多。