四则运算的例子
antlr4是一个非常通用,也非常强大的解释器的生成工具,它涵盖了词法分析和语法分析的内容,使用简单,功能强大,只需要配置一个g4文法文件,即可完成代码生成。这是一个java语言写的库,但是能生成各种语言的代码。通过pip install antlr4即可安装命令行指令。
下面就是官方介绍给的例子,是一个四则运算的例子。
// 与文件同名
grammar Calc;
// 程序 就是一个表达式然后结束
prog: expr EOF ;
// 表达式可以使数字、括号、嵌套乘除或加减
// 注意#MulDiv这一部分不能忽略,他会作为一个生成程序时候对应的方法名
// 注意op=xxx这个写法本来可以直接写成('+'|'-'),但是这样很难维护
expr
: expr op=(MUL|DIV) expr # MulDiv
| expr op=(ADD|SUB) expr # AddSub
| INT # Int
| '(' expr ')' # Parens
;
NEWLINE : [\r\n ]+ -> skip;
INT : [0-9]+ ;
ADD: '+';
SUB: '-';
MUL: '*';
DIV: '/';
通过指令antlr4-parse Calc.g4 -gui可以查看生成的语法树。

通过指令antlr4 calc.g4可以生成代码,默认是生成java代码,可以通过-Dlanguage=Python3指定生成python代码,目前支持10+种语言可到官网查看,这里我们就以java为例。运行后生成了6个java文件2个interp文件,2个tokens文件,其中interp和tokens文件是辅助文件,帮助理解运行过程,不需要可删除。
📦antlr-demo
┣ 📜Calc.g4
┣ 📜Calc.interp
┣ 📜Calc.tokens
┣ 📜CalcBaseListener.java
┣ 📜CalcBaseVisitor.java
┣ 📜CalcLexer.interp
┣ 📜CalcLexer.java
┣ 📜CalcLexer.tokens
┣ 📜CalcListener.java
┣ 📜CalcParser.java
┗ 📜CalcVisitor.java
这里建议下载antlr4-tool的idea插件,并进行如下配置
因为antlr4主要工作是词法分析和语法分析,所以想要最终解释运行,还需要自己实现一个解释器。
import org.antlr.v4.runtime.*;
import org.antlr.v4.runtime.tree.*;
public class CalcInterpreter extends CalcBaseVisitor<Integer> {
@Override
public Integer visitAddSub(CalcParser.AddSubContext ctx) {
int left = visit(ctx.expr(0));
int right = visit(ctx.expr(1));
if (ctx.op.getType() == CalcParser.ADD) {
return left + right;
} else {
return left - right;
}
}
@Override
public Integer visitMulDiv(CalcParser.MulDivContext ctx) {
int left = visit(ctx.expr(0));
int right = visit(ctx.expr(1));
if (ctx.op.getType() == CalcParser.MUL) {
return left * right;
} else {
return left / right;
}
}
@Override
public Integer visitProg(CalcParser.ProgContext ctx) {
return visit(ctx.expr());
}
@Override
public Integer visitInt(CalcParser.IntContext ctx) {
return Integer.valueOf(ctx.INT().getText());
}
@Override
public Integer visitParens(CalcParser.ParensContext ctx) {
return visit(ctx.expr());
}
public static void main(String[] args) throws Exception {
String input = "1 + 2 * 3";
CalcLexer lexer = new CalcLexer(CharStreams.fromString(input));
CalcParser parser = new CalcParser(new CommonTokenStream(lexer));
ParseTree tree = parser.prog();
CalcInterpreter visitor = new CalcInterpreter();
Integer result = visitor.visit(tree);
System.out.println("Result: " + result); // 打印 7
}
}
然后当我们运行antlr4 calc.g4的时候,会发现他下载了一个jar包,我们找到这个jar包,找不到直接从maven下载一个也行,这里建议是直接新建一个maven项目,用IDEA打开,把生成的java文件和上面解释器java类,都拷贝到项目中,并在项目中引入antlr4的依赖。
<dependency>
<groupId>org.antlr</groupId>
<artifactId>antlr4</artifactId>
<version>4.13.2</version>
</dependency>
一些概念解释
g4文件是一种上下文无关文法的表示。prog是入口的名字,可以定义为别的,对应代码中parser.prog(),改成别的名字,生成代码也会跟着改。expr中后面用了#XXX,对应生成的代码中会有visitXXX这样比较方便expr中op=(ADD|SUB),op=会在上下文中增加一个op变量名,这样方便判断。而op的取值专门定义了ADD等名称,这样会生成枚举,同样是为了代码直观。antlr最强大的就是递归匹配,expr中乘除法要写到加减法前面,这样1+2*3才能把2*3先结合。PLUS这种大写字母的,是词法分析的TOKEN在词法分析阶段识别。小写开头的才是语法分析规则。
g4中是允许递归的,例如exp: exp + exp | INT;,这里exp是递归的。但是g4不允许间接的最左递归,什么叫最左递归,就是第一个元素是递归的,上面exp配置中最左元素就是exp,所以是最左递归,但是他是直接最左递归,也就是递归的是自己,这是合法的。但是如果是exp: mulexp + mulexp; mulexp: exp * exp;这样就不行了,在mulexp定义中,最左元素是exp,而exp最左元素又是mulexp,这就形成了间接最左递归,这是不允许的,这与g4的递归运行机制有关,间接最左递归会导致无线循环。
一个错误的用法如下,看似只是把加减法单独拆到了infixExpr中定义,但是实际上会引起无限递归
expr: infixExpr | INT;
infixExpr: expr (PLUS | MINUS) expr;
运行报错
error(119): Calc.g4::: The following sets of rules are mutually left-recursive [expr, infixExpr]
正确的一种写法如下:
// 中缀运算符
expr: infixExpr;
// 中缀运算符最低优先级是 +-,直接指向+-表达式
infixExpr: addSubExpr;
// +-表达式可以是个*/表达式,或者+-表达式 与 乘除表达式通过+-符号连接
addSubExpr
: mulDivExpr
| addSubExpr op=(ADD|SUB) mulDivExpr;
// 乘除表达式可以是个数字,或者乘除表达式与数字结合。
mulDivExpr
: INT
| mulDivExpr op=(MUL|DIV) INT;
这个是标准的分层写法,他很好的诠释了优先级,比较难理解的是为什么加减表达式里有乘除表达式,这种写法其实是深度优先,让优先级高的先运行,所以addSub->mulDiv->INT会依次作为前者的一个可能匹配项,另一个匹配项是当前元素与高优先级元素通过op结合,在addSub中是不能向上引用infixExpr或expr的会导致无限递归。
当输入字符为1纯数字的时候,词法分析是INT,然后会自顶向下的依次匹配,发现是expr->infixExpr->addSubExpr->mulDivExpr->INT,最终INT是匹配的,他同时还有4个父类型。
当输入字符是1 + 2 * 3的时候,先进行词法分析,1=》INT;+=》ADD;2=》INT;*=》MUL;3=》INT;然后语法分析匹配,自顶向下到addSubExpr这一层,发现有ADD,所以1应该去匹配addSubExpr(最后匹配成功),而2*3应该去匹配mulDivExpr,也匹配成功。
当输入自复式1+2*3+4的时候,直接到语法分析1匹配addSubExpr,2*3+4匹配mulDivExpr,此时发现匹配失败了,所以addSubExpr这一层按照第一个+进行拆分左右元素是不可行的。接下来有两种情况,一种是1+2*3+4直接按照mulDivExpr去匹配,这个其实应该在这一步之前去尝试的,当然也是尝试失败的。所以最后一种情况就是继续往后找,看有没有+/,发现是有的,那1+2*3按照addSubExpr匹配(成功),4按照mulDivExpr匹配(成功),所以最后匹配成功。
有人会想上面为什么不是addSubExpr op=(ADD|SUB) addSubExpr,既然可以自引用,为什么最后一项不是自己呢?自己是mulDivExpr的超集。
这个问题非常重要,上面最后这个1+2*3+4的匹配过程或许可以解答。涉及到运算符优先级和左递归的结合性,正确的写法中暗含的意思是,乘除法的优先级是高于加减法的,另外处理过程中加减法是满足左侧结合的,避免解析后一个元素也是addSub导致的右侧结合的结果。(左结合意思是1+2+3先运算1+2,在运算(1+2)+3)。一般antlr的中缀运算符写法都是,左侧是自己,右侧是高一级优先级的表达式。
mocha
了解了上述知识,我们迎来第一个练习题,就是把之前手写的解释器的词法分析和语法分析部分,用antlr一个配置文件就搞定。
我们循序渐进,先把词法分析的token和语句定义完成,把最复杂的表达式解析放到后面。
grammar Mocha;
// 程序由多个语句组成
program: statement+ ;
// 语句由很多种
statement
: varStatement
| returnStatement
| blockStatement
| ifStatement
| forStatement
| breakStatement
| continueStatement
| throwStatement
| tryCatchStatement
| classStatement
| expresstionStatement
| ';'
;
varStatement: 'var' IDENTIFIER '=' expression ';' ;
returnStatement: 'return' expression ';' ;
throwStatement: 'throw' expression ';';
expresstionStatement: expression ';' ;
blockStatement: '{' statement* '}' ;
ifStatement: 'if' '(' cond=expression ')' ifBody = blockStatement ('else' elseBody=blockStatement)? ;
forStatement: 'for' '(' init=statement cond=statement step=expression ')' body=blockStatement;
breakStatement: 'break' ';';
continueStatement: 'continue' ';';
tryCatchStatement: 'try' tryBody=blockStatement 'catch' '(' IDENTIFIER ')' catchBody=blockStatement;
NULL: 'null';
TRUE: 'true';
FALSE: 'false';
NEW: 'new';
FUNCTION: 'function';
CONSTRUCTOR: 'constructor';
INCREMENT: '++';
DECREMENT: '--';
PLUS: '+';
MINUS: '-';
BNOT: '~';
EQ: '==';
ASSGIN: '=';
MULTIPLY: '*';
DIVIDE: '/';
MODULUS: '%';
POINT: '.';
OR: '||';
BOR: '|';
AND: '&&';
BAND: '&';
NEQ: '!=';
NOT: '!';
LTE: '<=';
LT: '<';
GTE: '>=';
GT: '>';
COMMA: ',';
LPAREN: '(';
RPAREN: ')';
LBRACE: '{';
RBRACE: '}';
LBRACK: '[';
RBRACK: ']';
SUPER: 'super';
NUMBER: [0-9]+('.' [0-9]+)? ;
STRING: ('"' ( ~["\\] | '\\' . )* '"') | ('\'' ( ~['\\] | '\\' . )* '\'');
IDENTIFIER: [a-zA-Z_][a-zA-Z_0-9]* ;
EMPTY: [\t\r\n ]+ -> skip;
// 单行注释
LINE_COMMENT: '//' ~[\r\n]* -> skip ;
// 多行注释
BLOCK_COMMENT: '/*' .*? '*/' -> skip ;
对于上面的代码,其实没什么好解释的,主要是对于一些语句的格式进行了定义,以及定义了一些词法分析的TOKEN,当然这里注意到我们没有对ClassStatement的定义,因为他比较复杂,基础形式是这样的class XX [extends XX] {},在{}中可以有两种声明一种是字段声明,格式是fieldName;或者fieldName = value;。另一种是方法声明,格式是methodName(params) {xxx},但是方法中有一个比较特殊的方法是constructor这个方法呢,我们要求他的第一行必须是super(params)。思考一下如何定义这样一个语句呢?下面是代码:
// 类声明
classStatement
: 'class' className=IDENTIFIER
('extends' parentName=IDENTIFIER)? // 可选的extends
'{' classBody '}'
;
// 类体
classBody
: (classElement)* (constructorDeclaration)* (classElement)* // 允许空类体,或多个元素
;
// 类元素可以是字段、方法或构造函数
classElement
: fieldDeclaration
| methodDeclaration
;
// 字段声明
fieldDeclaration
: IDENTIFIER (ASSGIN expression)? ';'?
;
// 方法声明
methodDeclaration
: IDENTIFIER '(' params ')' blockStatement ';'?
;
// 构造函数声明
constructorDeclaration
: CONSTRUCTOR '(' params ')' '{' constructorBody '}'
;
// 构造函数体
constructorBody
: superCall statement* // 在语义分析时检查super(xx)必须存在且为第一句
;
// super调用
superCall
: 'super' '('(expression ','?)* ')' ';'
;
接下来是表达式,自顶向下,按照优先级进行排序,写法与前面提到的四则的分层优先级写法是一样的。依次是assignExpression andExpression eqExpression compExpression additionExpression multiplicationExpression prefixExpression postfixExpression functionOrPointExpression和unary。这里面有较多的细节需要分别解释。
expression
: assignExpression;
assignExpression
: andExpression # AndInAssign
| leftValue op=ASSGIN right=assignExpression # Assign
;
// 左值表达式
leftValue
: IDENTIFIER # LeftUnary
| leftValue ('(' (expression ','?)* ')') '.' IDENTIFIER # PropertyAccessInFunCall
| leftValue '.' IDENTIFIER # PropertyAccess
| leftValue ('(' (expression ','?)* ')') '[' index=expression ']' # ArrayAccessInFunCall
| leftValue '[' index=expression ']' # ArrayAccess
;
andExpression
: eqExpression # EqInAnd
| left=andExpression op=(AND|OR) right=eqExpression # And
;
eqExpression
: compExpression # CompInEq
| left=eqExpression op=(EQ|NEQ) right=compExpression # Eq
;
compExpression
: additionExpression # AddInComp
| left=compExpression op=(LTE|GTE|LT|GT) right=additionExpression # Comp
;
additionExpression
: multiplicationExpression # MulInAdd
| left = additionExpression op=(PLUS|MINUS) right = multiplicationExpression # Add
;
multiplicationExpression
: prefixExpression # PreInMul
| left = multiplicationExpression op=(MULTIPLY|DIVIDE|MODULUS) right = prefixExpression # Mul
;
prefixExpression
: postfixExpression # PostfixInPrefix
| op=(PLUS|MINUS|NOT|BNOT|INCREMENT|DECREMENT) right=postfixExpression # Prefix
;
postfixExpression
: functionOrPointExpression # FunCallInPost
| left=functionOrPointExpression op=(INCREMENT|DECREMENT) # Postfix
;
functionCallOrPointExpression
: left=functionCallOrPointExpression '(' (expression','? )* ')' # FunCall
| left=functionCallOrPointExpression '.' IDENTIFIER '(' (expression','? )* ')' # PointFunCall
| left=functionCallOrPointExpression '.' IDENTIFIER # PointProperty
| left=functionCallOrPointExpression '[' index=expression ']''(' (expression','? )* ')' # IndexFunCall
| left=functionCallOrPointExpression '[' index=expression ']' # IndexProperty
| unary # UnaryInFunCallOrPoint
;
unary
: NUMBER #Number
| STRING #String
| NULL #Null
| TRUE #True
| FALSE #False
| SUPER #Super
| IDENTIFIER#Ident
| array # ArrInUnary
| group #Gro
| object #ObjInUnary
| function #FunInUnary
| new #NewInUnary
;
group: '(' expression ')';
array
: '[' (expression (',' expression)* ','?)? ']'
;
object: '{' (pair','?)* '}' ;
pair: key=(STRING | IDENTIFIER) ':' value=expression ;
function: FUNCTION '(' params ')' blockStatement;
params: (IDENTIFIER (',' IDENTIFIER)*)?;
new: NEW IDENTIFIER '(' (expression (',' expression)*)? ')';
首先assignExpression就是一个比较特殊的表达式,赋值语句有两点比较特殊,一是left元素的形式并非是自身,也并非是一个单元组,而是特定形式的左值表达式leftValue,可以是单元的表达式例如变量a,也可以是obj.a或者obj["x"].a.b等形式。另一个特殊的就是=运算符是右结合的,a=b=c等价于a=(b=c),默认的写法:
// 默认的优先级分层写法中,right=下一优先级,这样是按照左结合的
// 但是左值的形式是有限的,不能设置为assignExpression
assignExpression: andExpression
| assignExpression op=ASSGIN right=andExpression
// 将左值改为leftValue,right修改为assignExpression,递归的原因此时刚好实现右侧结合
assignExpression: andExpression
| leftValue op=ASSGIN right=assignExpression
右结合:
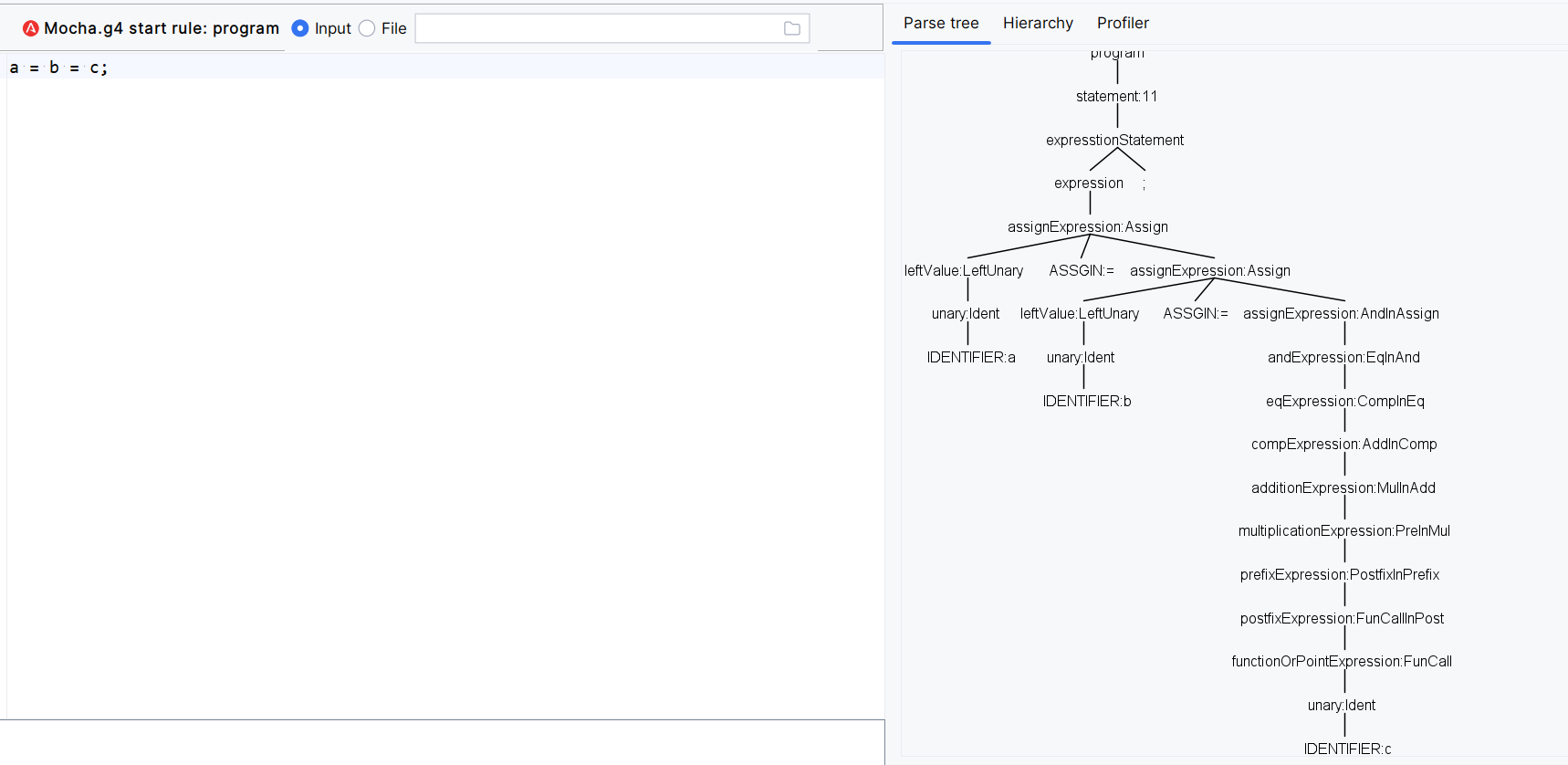
后面几个表达式都是模板的写法,直到prefixExpression这是前缀表达式,前缀是没有left的,而postfixExpression后缀是没有right的,后缀的优先级比前缀高,我们的语言中是支持如下写法的。
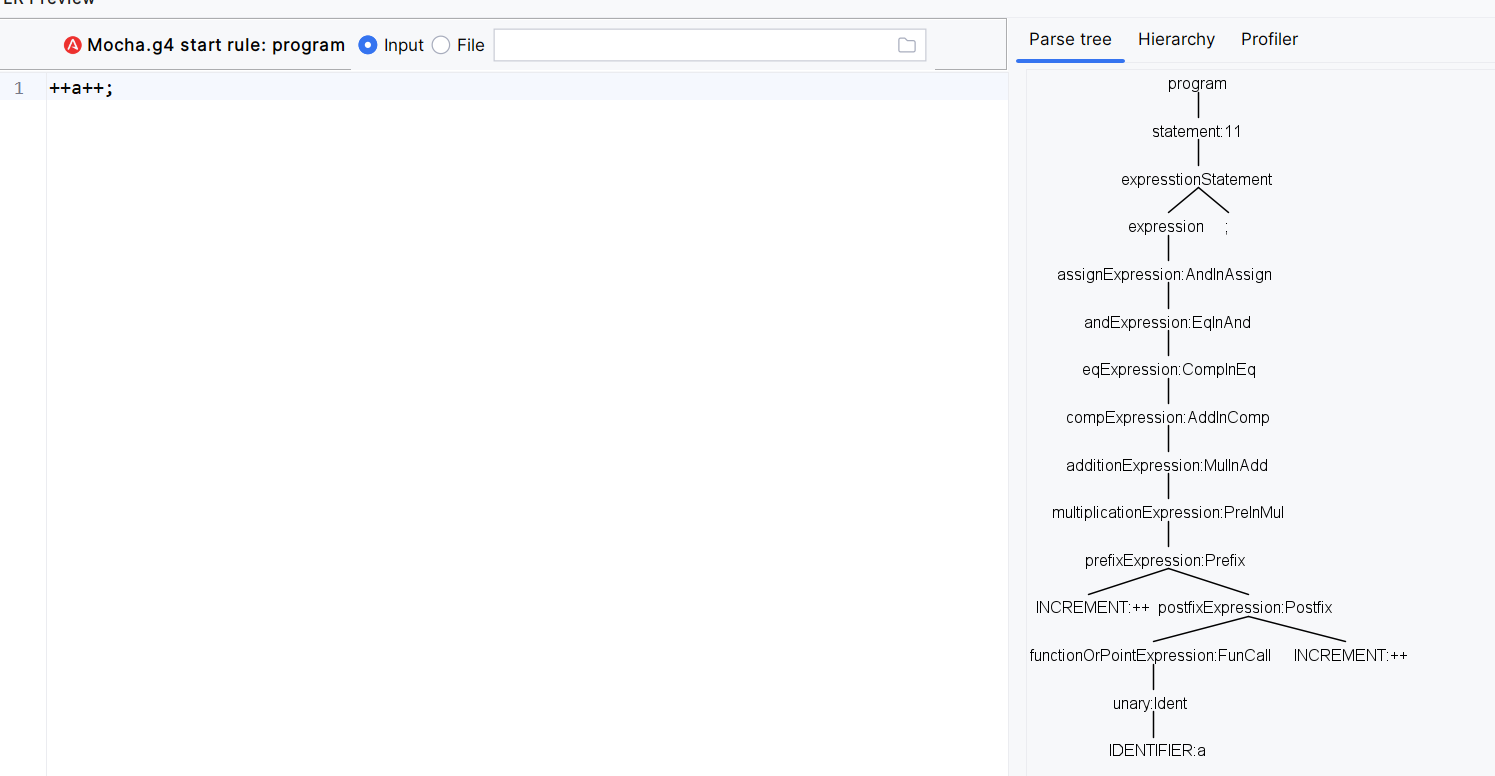
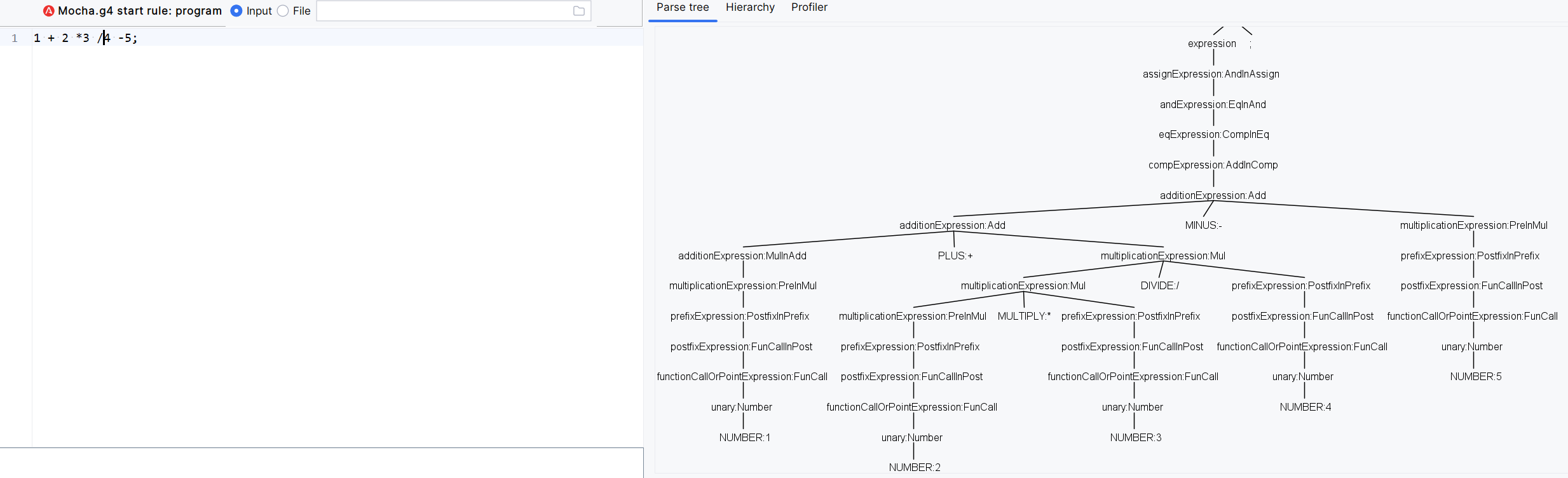
接下来是functionCallOrPointExpression函数调用和点表达式,函数调用按理说都是单元表达式,应该直接归到unary中就可以了,为啥这里单独拆了一层,主要是原来写到unary里发现是有问题的。以及为啥和.运算符合并成一个表达式了。
首先.的优先级是比++要高,比如a.age++是(a.age) ++等价。所以点运算符是放到后缀运算符下面的,然后a.getAge()等价于(a.getAge)(),也就是.运算符,比函数调用的优先级也要高。如果我们把函数调用作为一种unary就会导致解析为a.(getAge()),所以就把函数调用和点运算符一起放到了当前这一层来进行判断。
// 例如 add() => left是add
left=functionCallOrPointExpression '(' (expression','? )* ')'
// 例如 a.getAge() => left是a,IDENTIFIER是getAge,此时left指向的是this,为后续解析提供方便
left=functionCallOrPointExpression '.' IDENTIFIER '(' (expression','? )* ')'
// 例如 a.age,这个放到了下面一层,是可以先解析后面有没有括号
left=functionCallOrPointExpression '.' IDENTIFIER
// []运算符和.运算符是类似的,这里不写
思考下,如果此时是a.b().c["a" + "b"].d,是如何正常解析的,如下图。正是不断的递归。
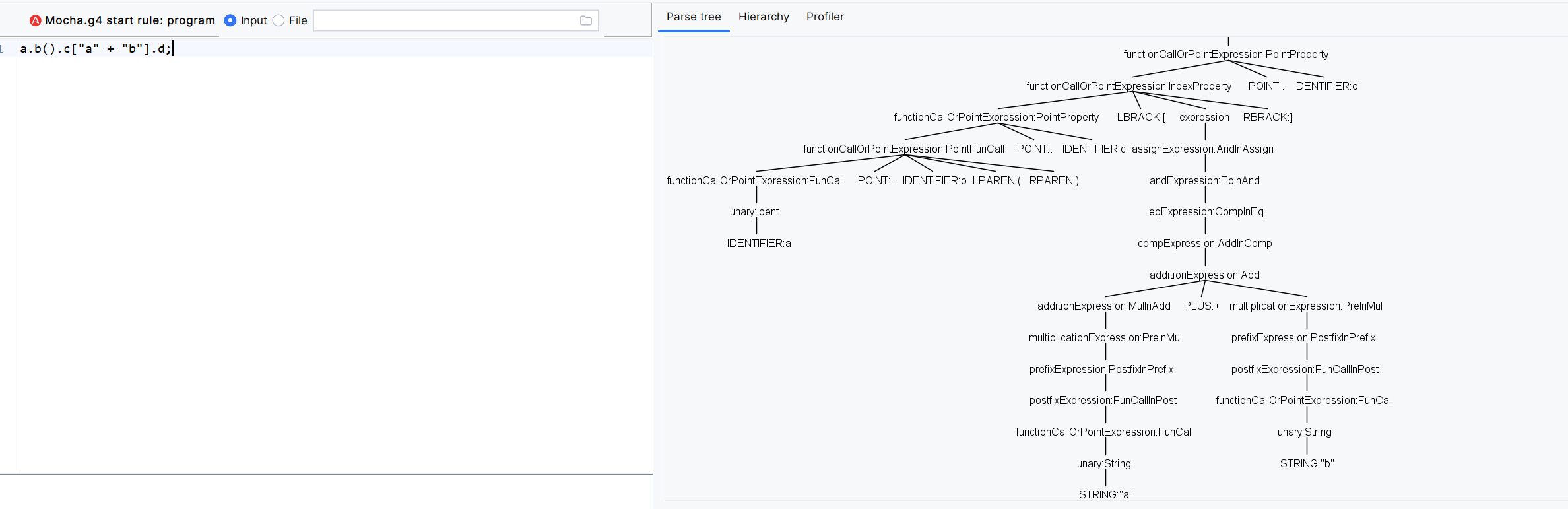
最后的unary就是剩余的单元运算,这里不再赘述,此外#xxx是为了生成代码中含有特定名称的hook函数,便于后续编程的。
基于上面的g4文件,我们用java实现以下mocha解释器,这部分放到下一篇文章中。